2D Non Projectile Motion
Learn how to do 2D non-projectile motion problems. Non projectile motion just means that the object is not in the air in freefall.
Describing and Determining Vector Components
- I know the difference between 1D and 2D motion
- I know the difference between non-projectile and projectile 2D motion
- I can visually draw out vector addition and a resultant
- I can name the direction of a 2D vector
- I can draw the direction of a 2D vector
- I can resolve a 2D vector for its components
Q1: What is the difference between 1D and 2D motion?

2D Non Projectile Motion
Q2: What is the difference between non-projectile and projectile 2D motion?

Scalars vs. Vectors
- Scalars just have magnitude
- Vectors have magnitude and direction
Common Vector Examples
- Displacement: 5 meters north
- Velocity: 5 meters per second north
- Acceleration: 5 meters per second squared north
An arrow, with a head and tail, is used to represent a vector
- Tail: where you started
- Head: where you ended with the direction

Drawing vectors addition: head to tail
You walk 10 m north followed by 5 meters north. What is your overall displacement?
Start with an origin dot
- Add the first vector
- Then add the next tail to the head of the last direction
The resultant is the overall description of the added vectors. The resultant of 10 m north and 5 m north is 15 m North.
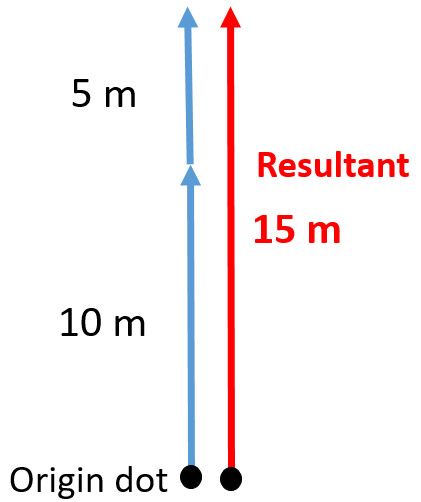
Head to Tail
It is important to draw vectors head to tail just like when following directions. To go to the mall you would not go back to the origin (beginning) before the next direction. The end of the last direction has an arrow tip head. The head of the last direction is where the tail of the new instruction begins every time.

Minimum and Maximum
When vectors are in the same plane, i.e. only X axis, the minimum displacement will be when they are in opposite directions. When vectors are facing the same direction the displacements add up. Pythagorean Theorem and Trigonometry functions SOH CAH TOA are used when vectors are not on the same plane. The rest of this page will show you how to do this.
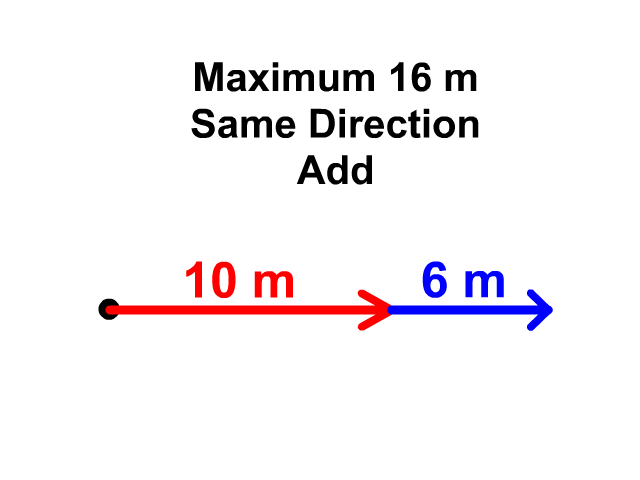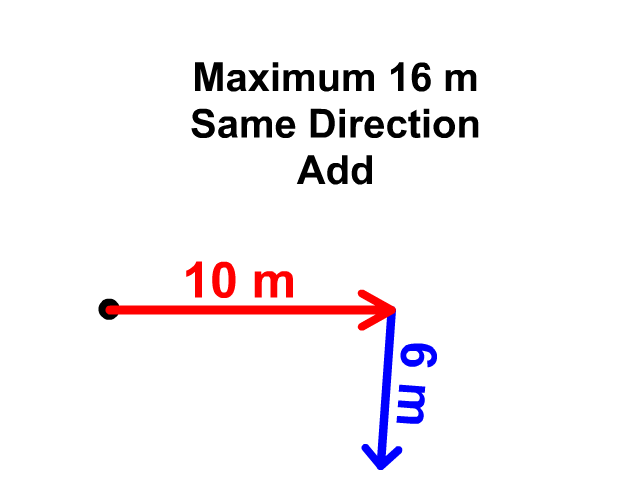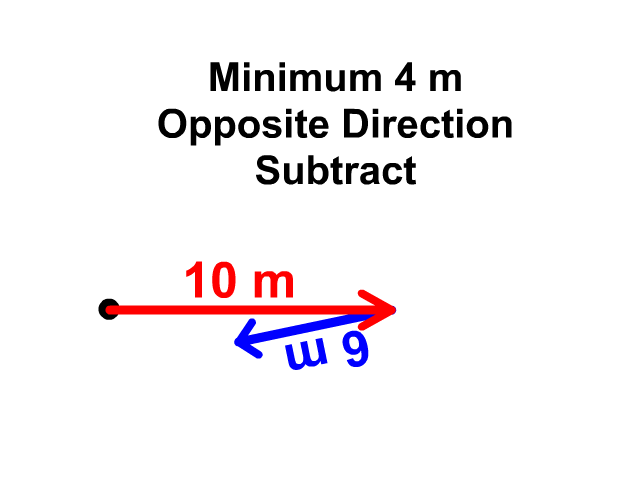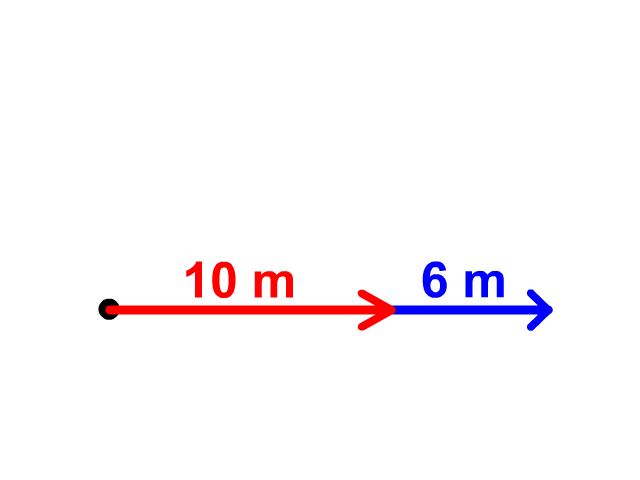
Q3: What is the minimum length of a 100 m and a 25 m vector added together?
Q4: What is the maximum length of a 100 m and a 25 m vector added together?
Q5: How would you place a 100 m and 25 m vector together to get the maximum displacement?
Either Vector First
When adding two vectors, 20 meters north and 40 meters east, you would start with an origin dot then draw them head to tail. It does no matter which one you draw first as long as they are head to tail. The magnitude will be the same either direction you follow first but you’ll have complimentary angles and descriptions. One may be 27° N of E and the other would be 63° E of N. Complimentary means the two add up to 90°.
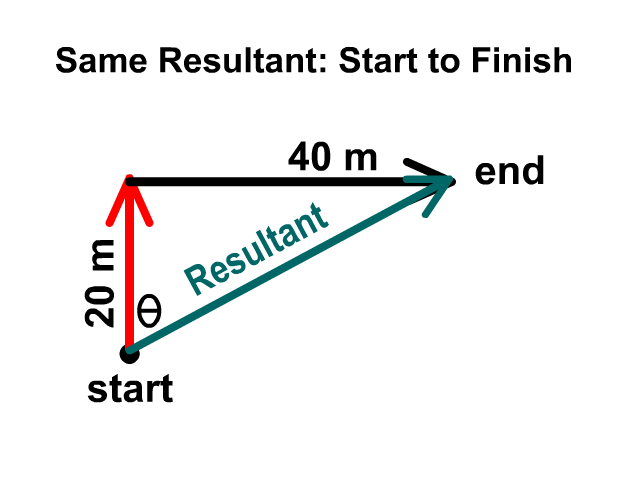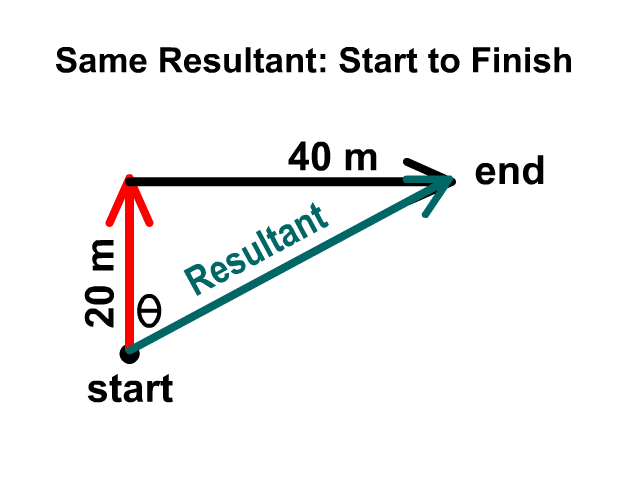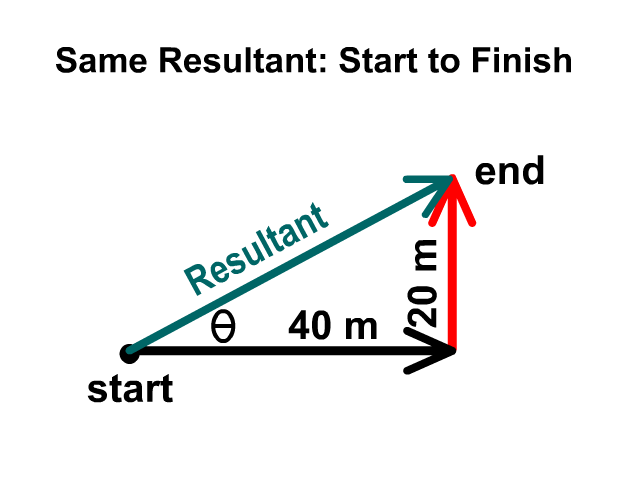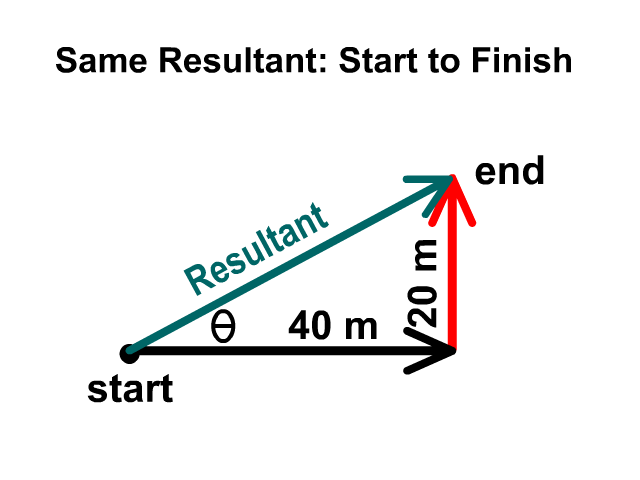
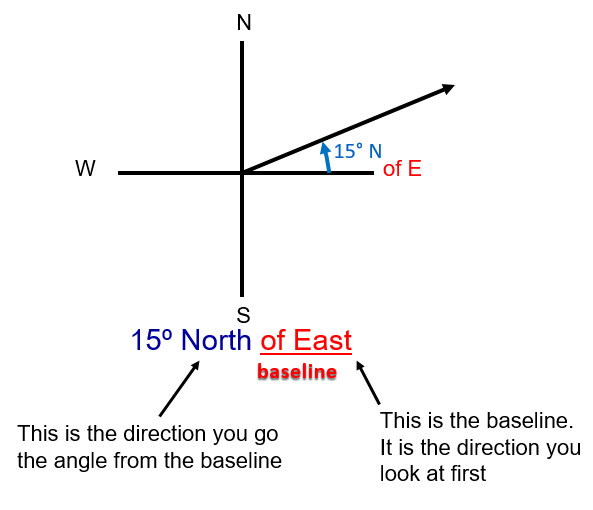
Describing The Direction
Directions have a baseline, starting direction from which the angle is directed, described many possible ways.
- From the +X axis
- East
- Right
- And Many Others
Look at the context of the problem to determine which to use.
The angle will be directed from that baseline and needs a direction as well. Look at the difference between 20° N of E and 20° N of W. Both are 20° north but without the baseline the direction is uncertain. Of east or of west is a baseline that completes the direction.
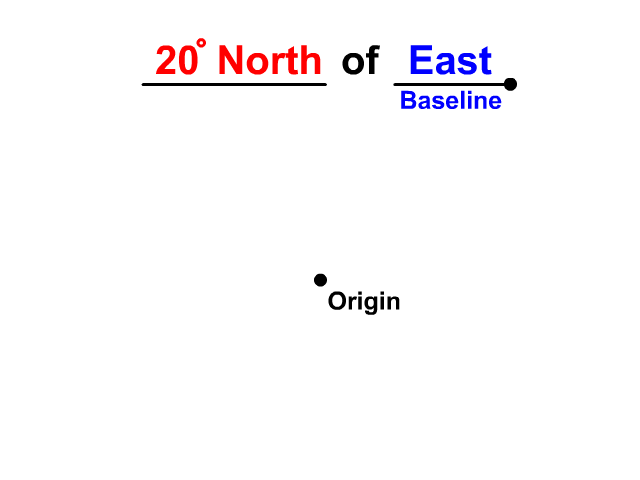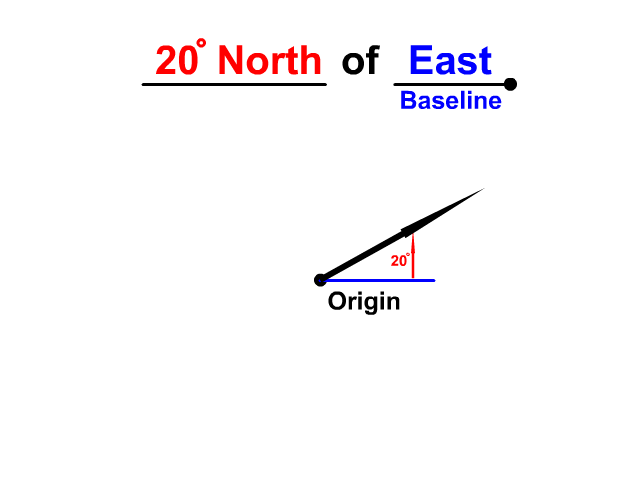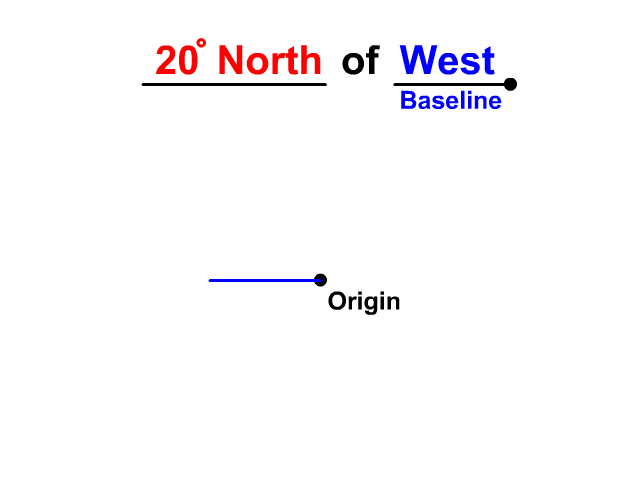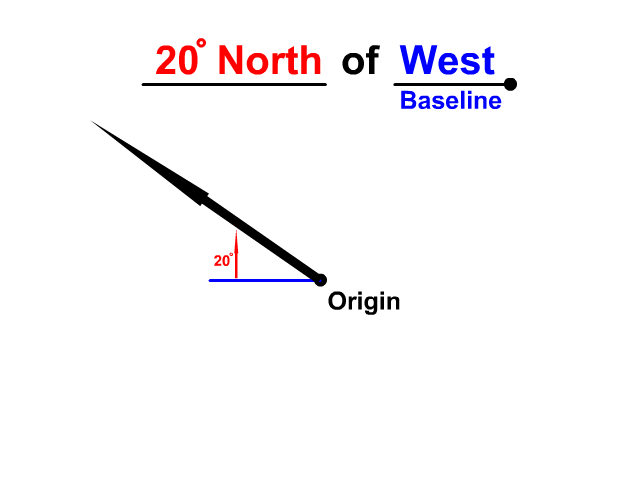
Describe the direction using north, east, south, west directions
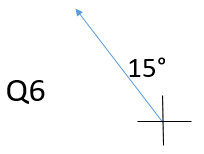
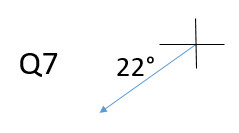
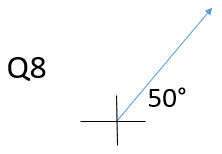
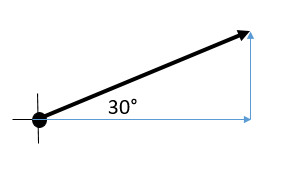
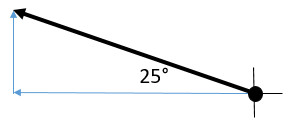
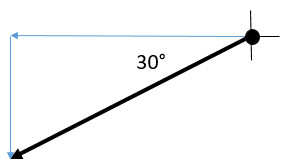
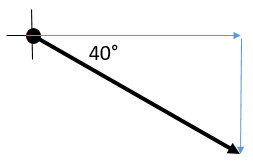
Describing directions: On each question, draw the vector arrow on the coordinate axis
Q9: 30° N of E
Q10: 25° N of W
Q11: 30° S of W
Q12: 40° S of E
Q13: 10° above the -X axis
Determining Components of a Vector
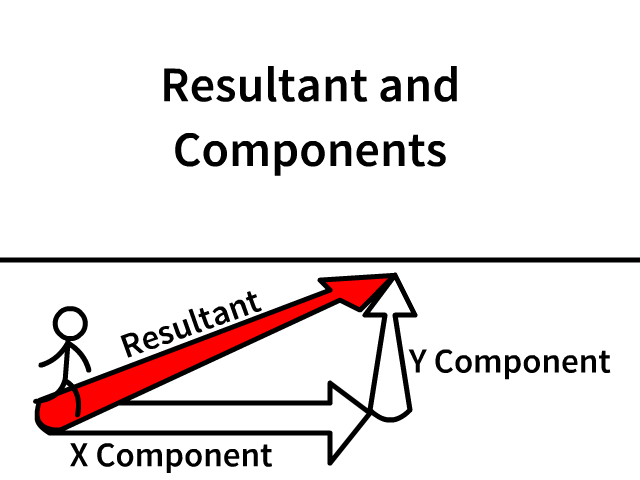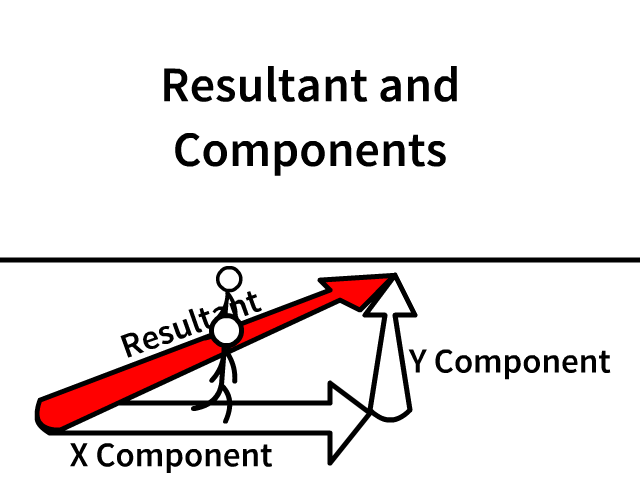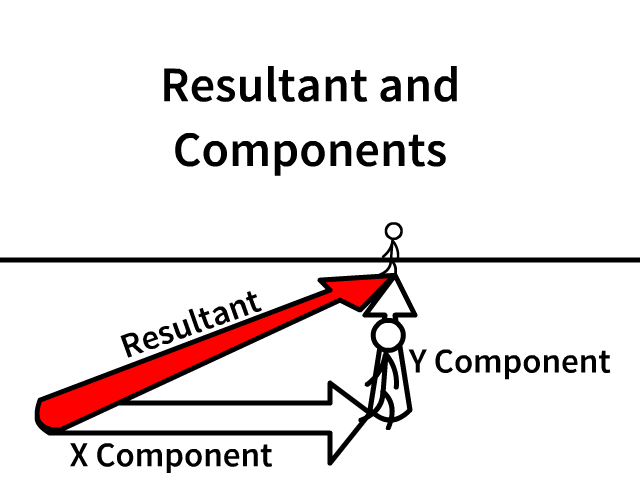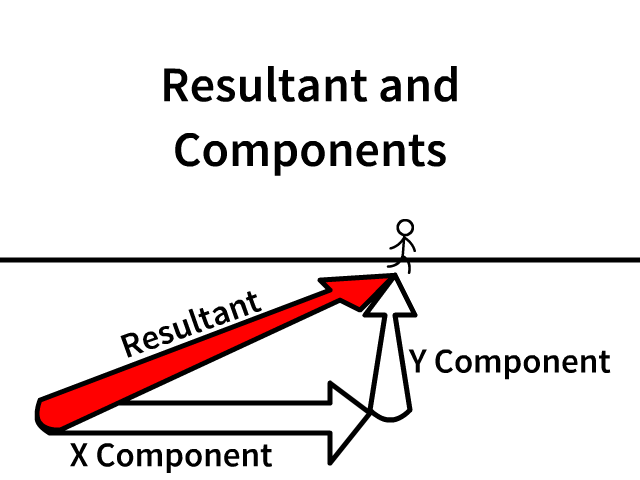
Resultant and X and Y Components
The resultant is the overall vector
Components lay along the X and Y axis
- Following the individual components lead you from the origin (staring point) to the same end
- Component arrows are always draw in the direction that would lead you from the same start to the same end
Trig Reminders
- The opposite of a triangle (a) and adjacent (b) change based on the location of the angle in question
- The hypotenuse is always the longest side
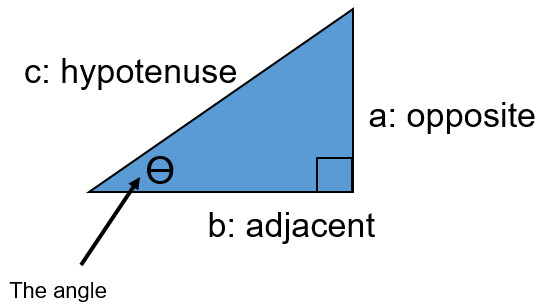
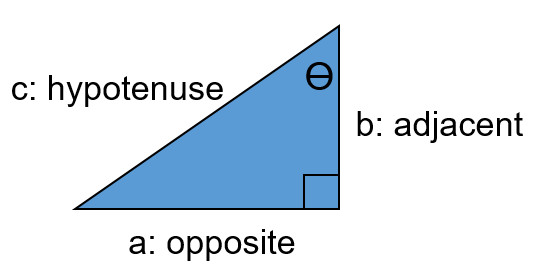
To determine a side with a right triangle when you know two other sides
- Use Pythagorean Theorem
a² + b² = c²
To determine an angle with a right triangle when you know two sides
Use what commonly is referred to a SOH CAH TOA
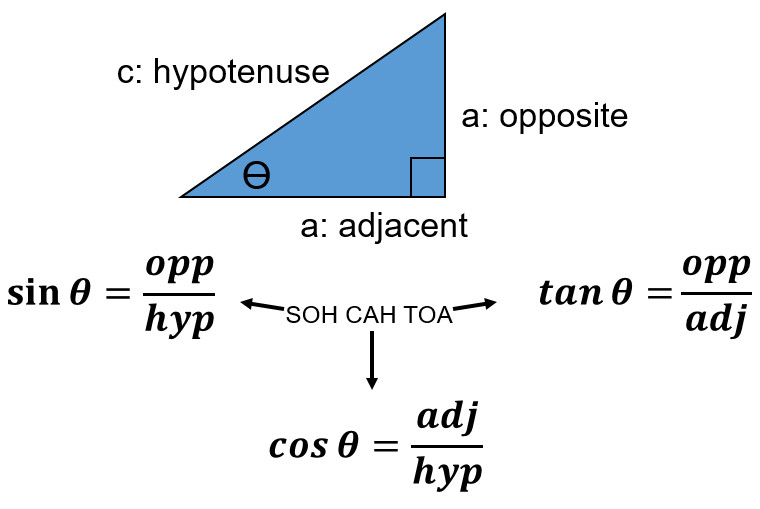
Calculator Check Time
Anytime you are going to be typing in Sin, Cos, Tan, etc. into a calculator and using degrees, be sure your calculator is on the degrees mode

Drawing out a Vector at an Angle and Solving for a Component
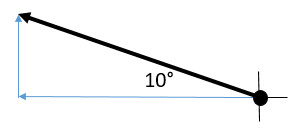
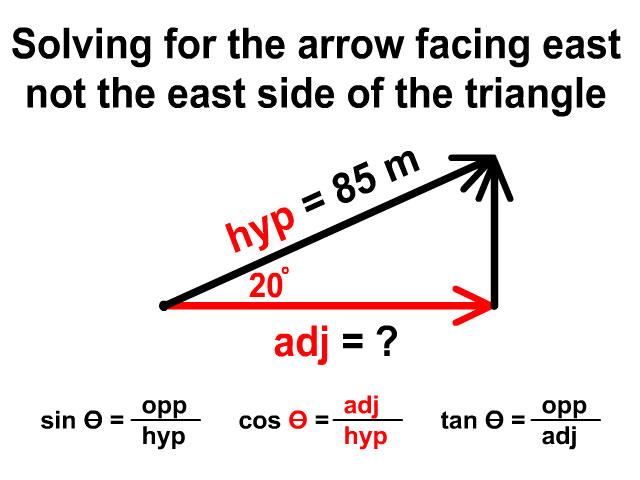
What is the east component of 85 m 20° North of East?
When you have a question like this you are trying to find a component of a vector. Because of being at an angle north of east, this vector will have a north component and east component that make it up. Follow the directions to solve for the east component of this vector.
- Draw an origin dot
- From the origin draw the last direction you see, east in this description (85m 20° North of East). Be sure to include the arrow tip. This represents your east component.
- Continue head to tail, draw the second to last direction, north in this description (85m 20° North of East). Also include an arrow tip. This represents your north component.
- Next draw the resultant, our hypotenuse. Go back to the origin and draw the arrow from start to finish. This represents the original vector described.
- Now place the 20° angle closest to the origin dot (85m 20° North of East)
- Lastly place the magnitude, 85m, on the hypotenuse.
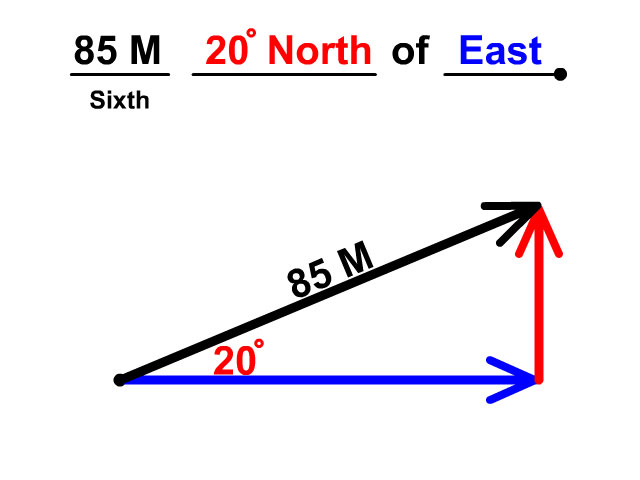
After drawing a vector, you have three arrows
- One on the hypotenuse which is the overall vector
- One in the X-Axis here the east component
- One in the Y-Axis here the north component
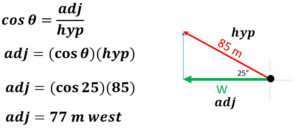
We are asked to solve for the east, so we will use our trig functions to figure out that side. The arrow in red is facing east and what we are solving for. We have the 85 m hypotenuse, a 20° angle, and the adjacent side as our unknown. This leads us to the cosine function which rearranges to adj = (cos Ө)(hyp).
adj = (cos Ө)(hyp)
adj = (cos 20)(85) = 80 m
The final answer to the question rounds to 35 meters east.
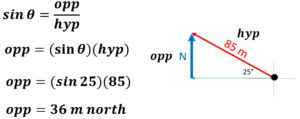
Example: What is the west component of 85 m 25° North of West?
Example: What is the north component of 85 m 25° North of West?
Problem Set
Try out the vector component problem set and use our video to check your answers to #1-#10
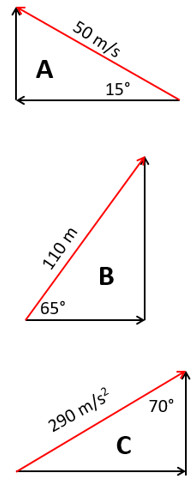
1. Find the X component of vector A
2. Find the north component of vector B
3. Find the east component of vector B
4. Find the Y component of vector C
5. Find the X component of vector C
6. What is the south component of 350 m/s 20° east of south?
7. What is the east component of 42 m 62° north of east?
8. What is the Y component of 28 m/s 21° South of West?
9. What is the east component of a wind that is blowing 15 mi/h 34° S of E?
10. What is the north component of 45 m/s 15° N of W?
Links
- Continue to part 2: Combining 2D Vectors
- Back to the Main 2D Motion Page
- Back to the Stickman Physics Home Page
- Equation Sheet