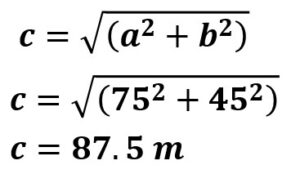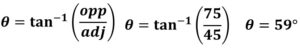Combining 2D Vectors

Home » Unit 2: Two Dimensional Motion: Projectile and Non-Projectile » Combining 2D Vectors

Learning Targets

I can to combine 2D vectors that lay on an X or Y axis to determine a resultant
I can to combine 2D vectors that don’t lay on an X or Y axis to determine a resultant
I can describe the resultant including a magnitude, angle, and description

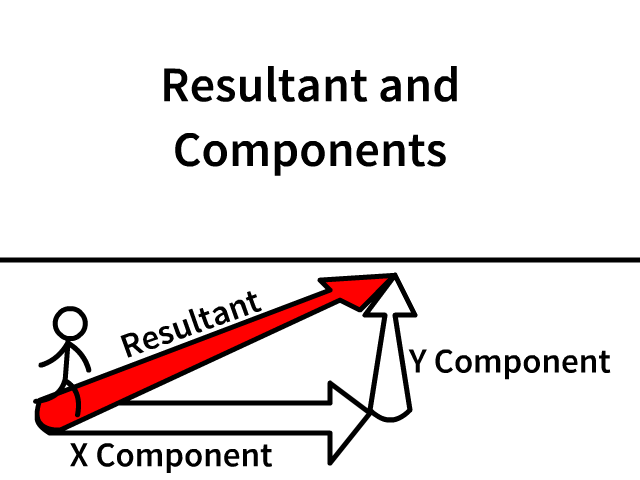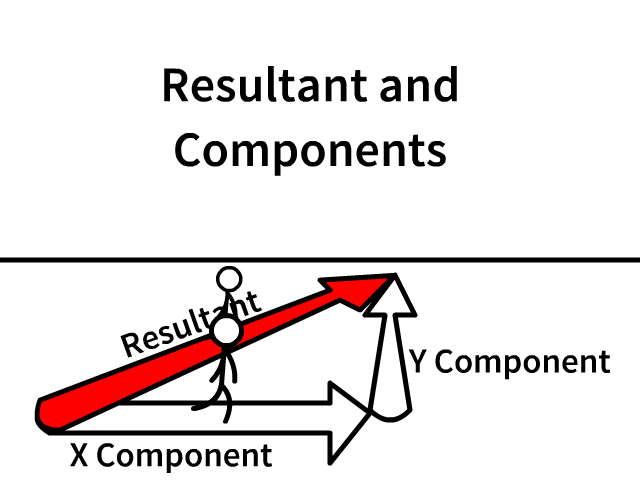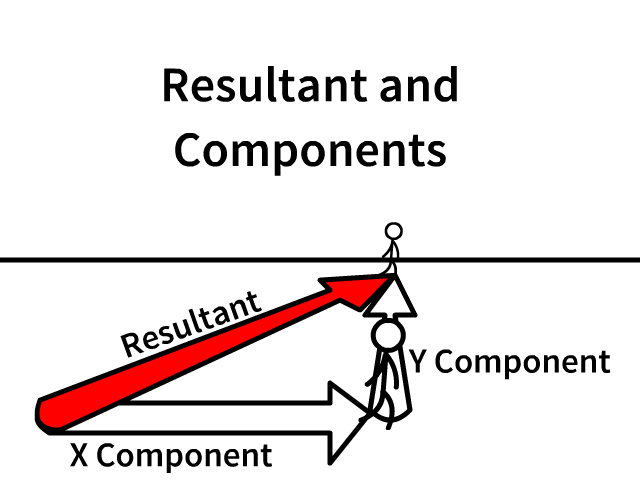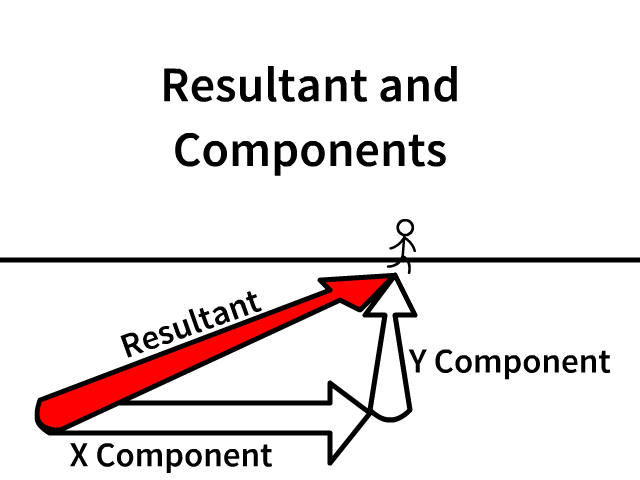
Resultant and Components

The resultant is the overall vector

Components are individual parts which create the resultant

Following the individual components lead you from the origin (staring point) to the same end
Component arrows are always draw in the direction that would lead you from the same start to the same end

In easier problems the components lay along the X and Y axis. In longer problems you start by breaking down vectors at angles to their X and Y components.

Observe the animation how the stickman is in the same position along the X or Y axis the whole time. The animation is following the X axis and then the Y axis. In reality the X and Y components are happening at the same time as the overall resultant.

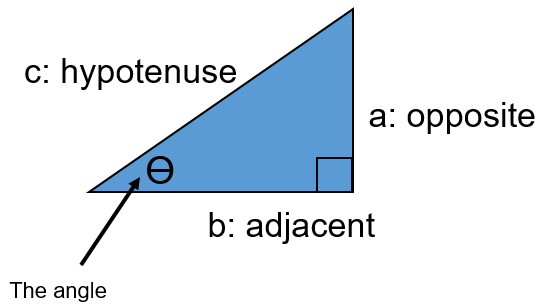
Trigonometry Reminders

Before we go any further be sure to remind yourself about how to solve for sides or angles of a right triangle. Also double check that your calculator is in degrees and not radians mode.

The opposite of a triangle (a) and adjacent (b) change based on the location of the angle in question
The hypotenuse is always the longest side

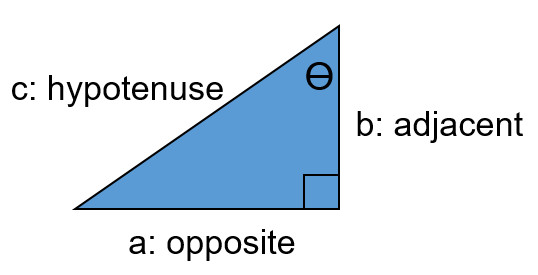
To determine a side with a right triangle when you know two other sides

Use Pythagorean Theorem

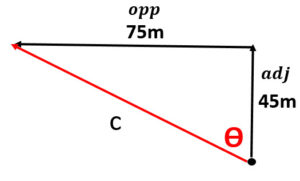
a² + b² = c²

To determine an angle with a right triangle when you know two sides

Use what commonly is referred to a SOH CAH TOA

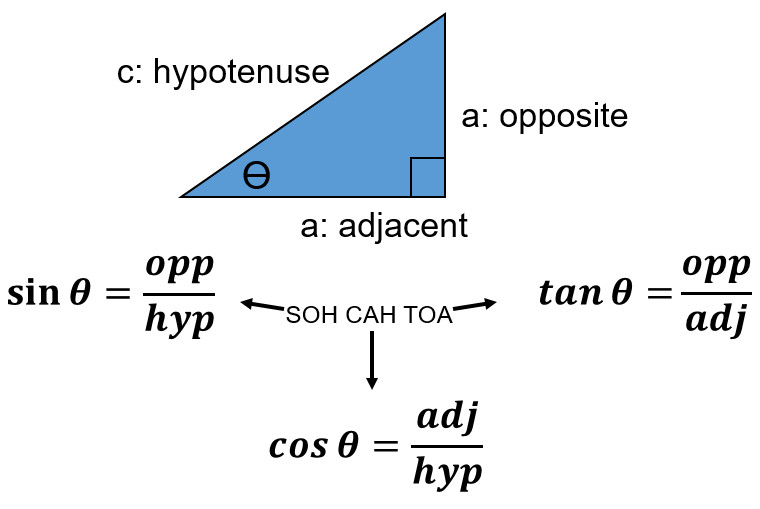
Calculator Check Time

Anytime you are going to be typing in Sin, Cos, Tan, etc. into a calculator and using degrees, be sure your calculator is on the degrees mode

Combining One X-Axis and One Y-Axis Vector to get a Resultant

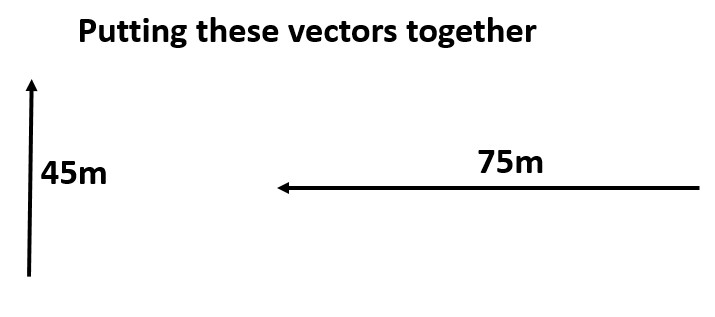
When adding two vectors on different axis, you can't simply add or subtract.

Follow the following steps to add vectors and get a three part magnitude, angle, and description of angle resultant answer.

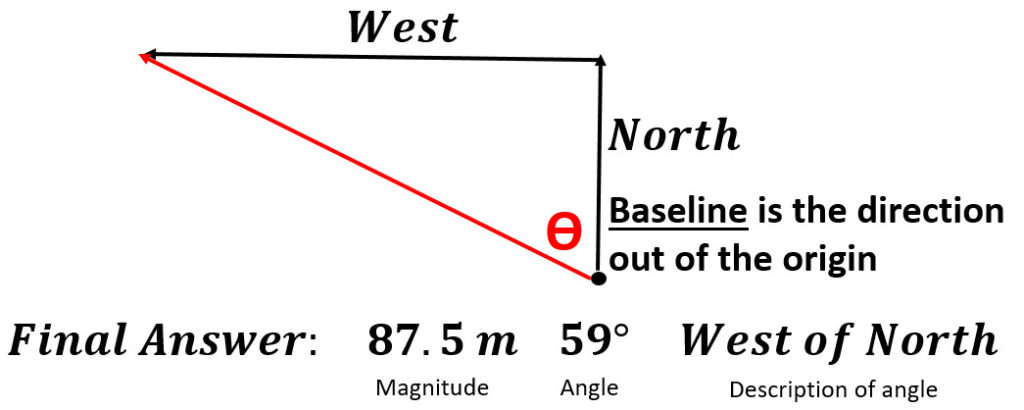
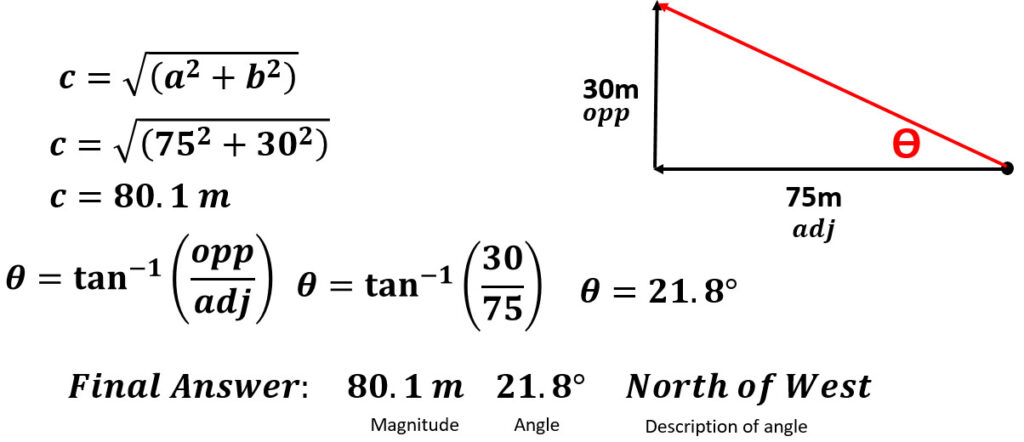
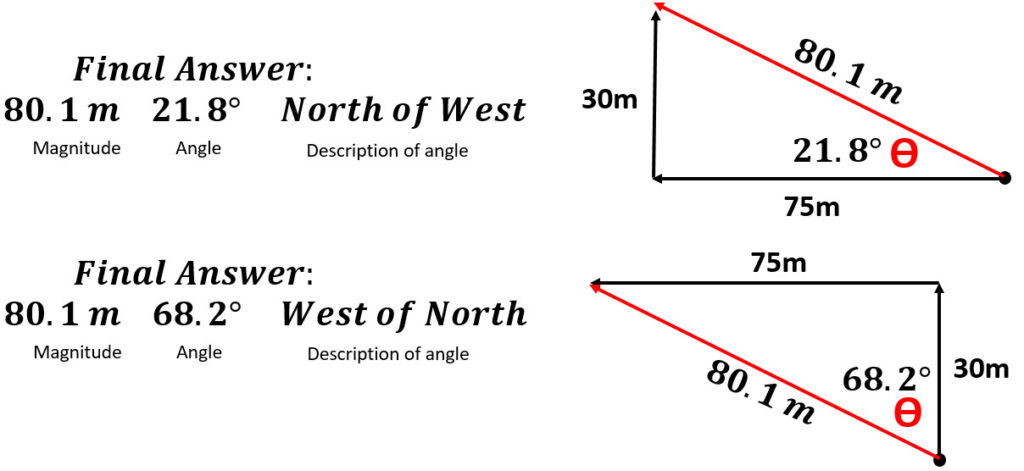
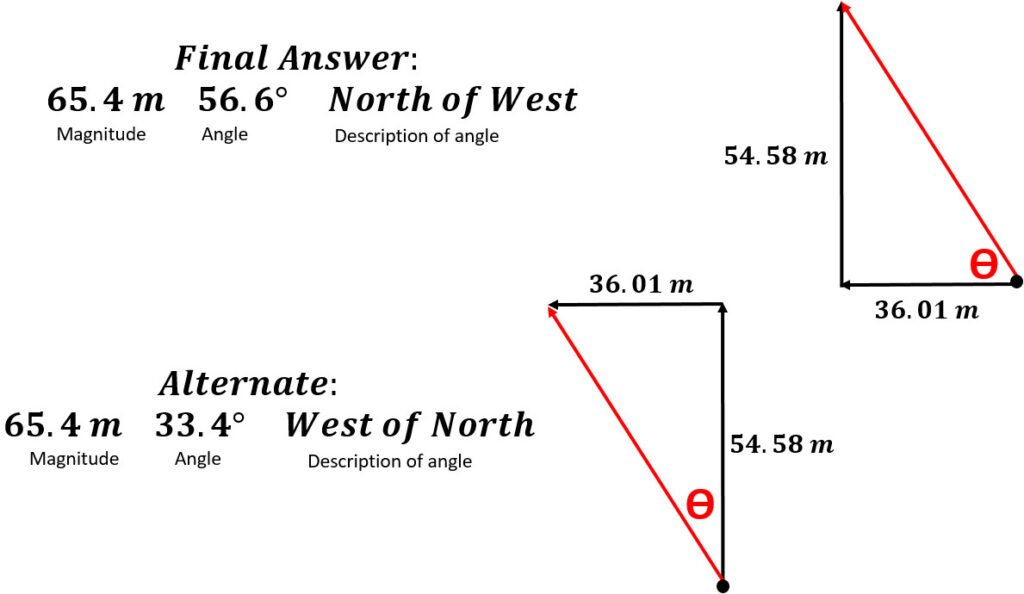
Example: What is the resultant of a horse that travels 45 meters north followed by 75 meters west?

1. Draw an origin dot

2. Draw the first component (45 meters north) and label it

3. Draw the next component (75 meters west) and label it starting at the previous arrow tip

4. Go back to the origin and draw the resultant from beginning to where the components ended.

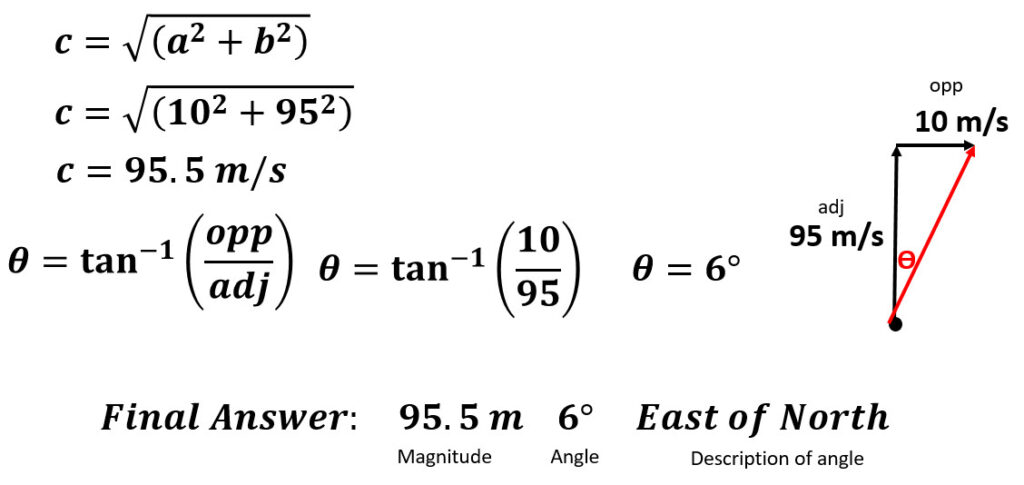
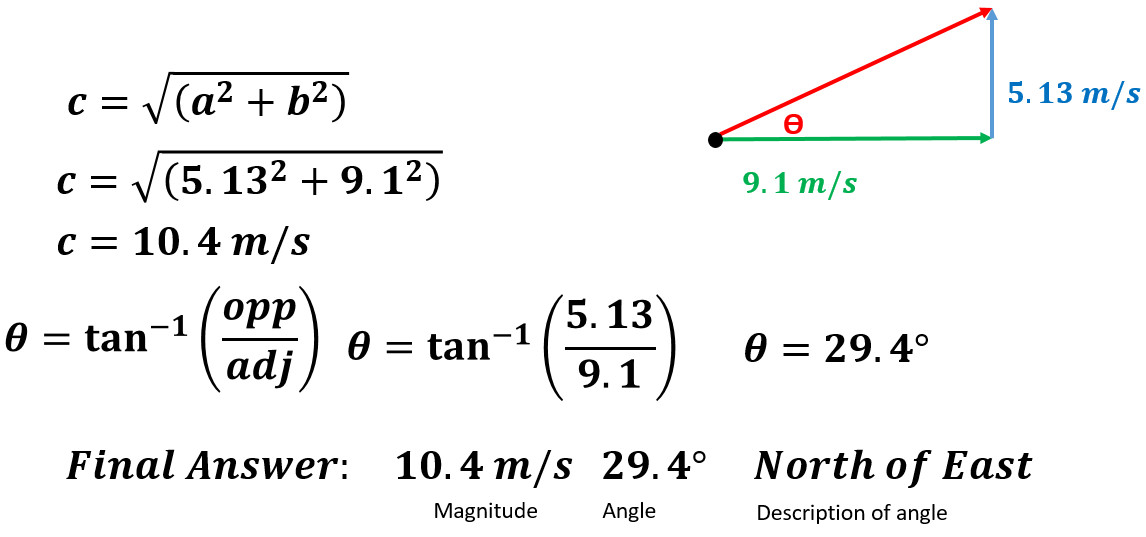
5. Use the Pythagorean Theorem to determine the hypotenuse.

6. Use inverse tangent to figure out the angle.

7. Describe the angle ____ of ____. The last direction is the baseline (line coming out of the origin dot) so W of N.

Practice:

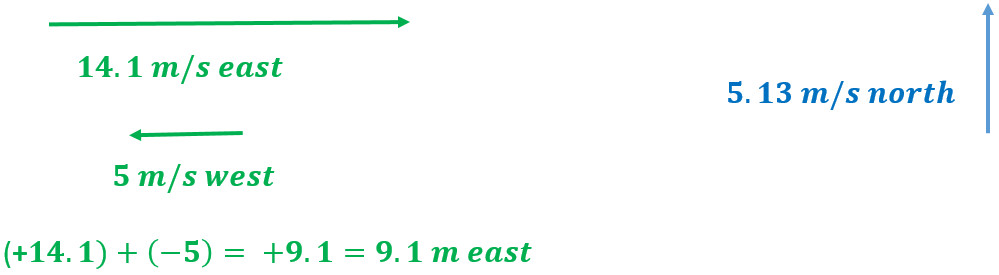
Q1: What is the result of flying 95 m/s north with a 10 m/s breeze blowing east?

Alternate Right Answer: 95.5 m 84° North of East

The alternate right answer would result from drawing the east vector first from the origin and then the north vector. 95.5 m 6º North of East would not be correct.

Combining More than two X-Axis and Y-Axis Vectors to get a Resultant

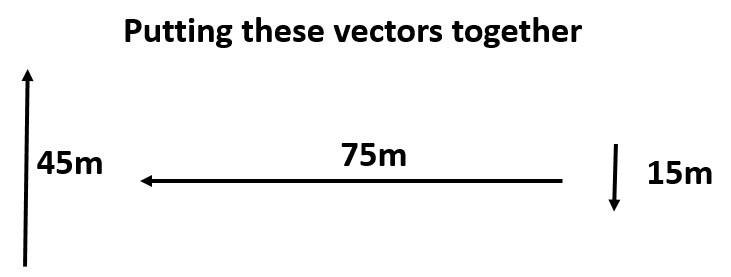
Example: What is the resultant of a person that travels 45 meters north, 75 meters west, and 15 meters south?

Start by putting any X components together as we did in the 1D motion section
- Here you only have a 75 m west component
Then put the Y components together as we did in the 1D motion section
- Here you have a 45 m north and 15 m south you will have to put together

X Axis:

75 m west

Y Axis:

45 m (+) north

15 m (-) south

(+45) + (-15) = +30 m or 30 m north

Now we have two overall vectors: 75 m west and 30 m north

Now draw an origin dot and use the resulting X then Y components
Then draw your resultant from origin to finish
Solve for the resultant magnitude, angle, and description of angle as we did in the prior problems

There are two alternative right answers depending if you drew the X axis component first or the Y axis component first.

Combining an off Axis Vector and One on Axis to get a Resultant

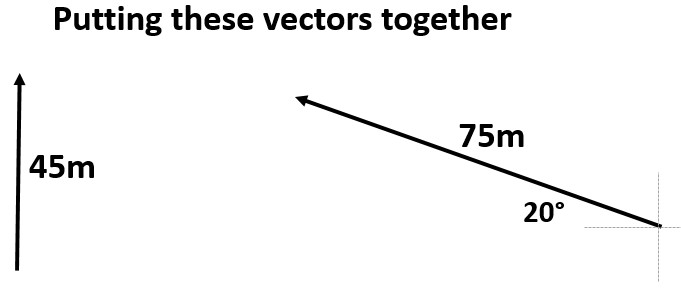
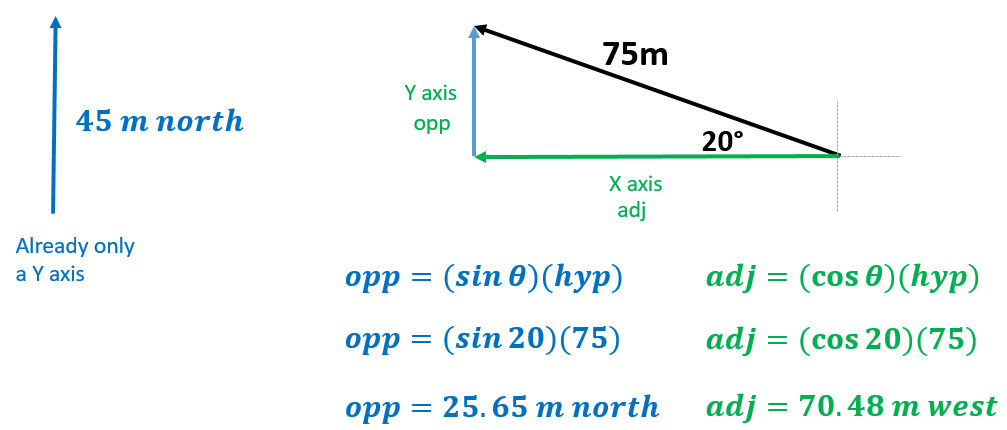
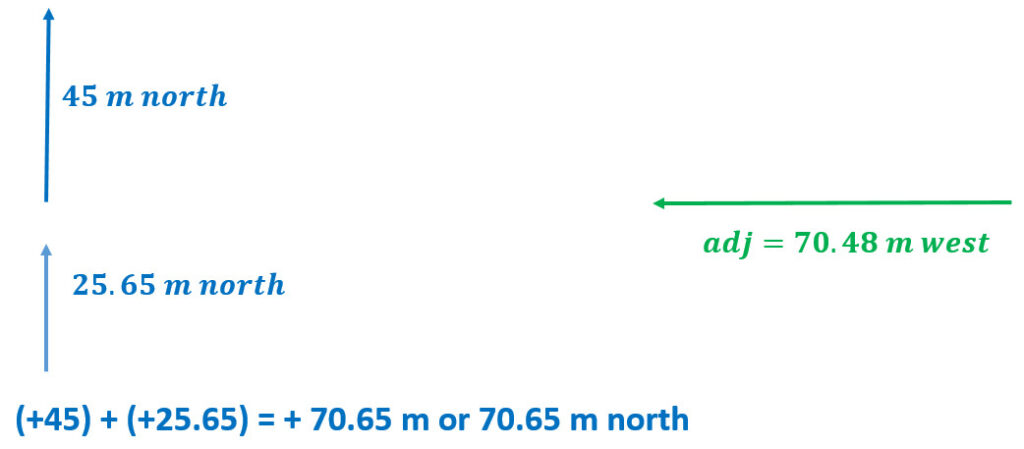
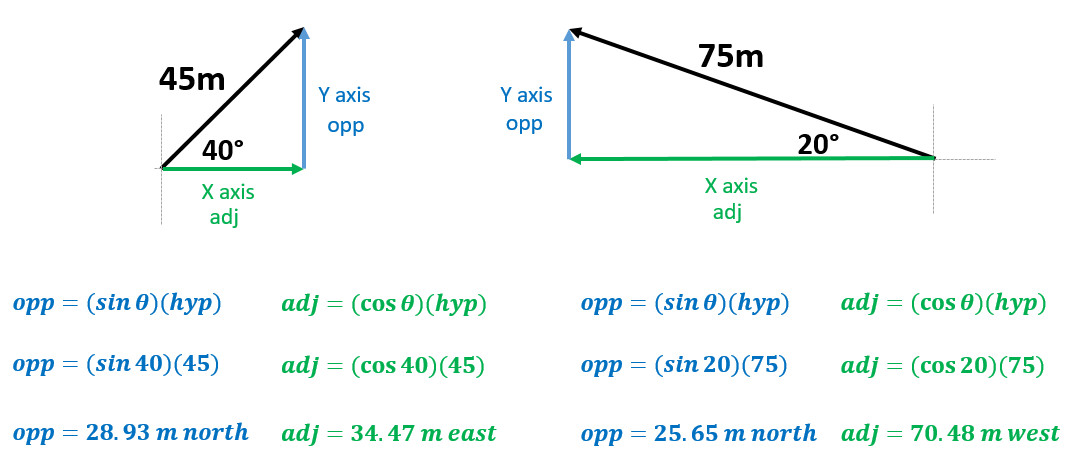
Example: Where is Joe located after traveling 45 meters North followed by 75 meters 20° North of West?

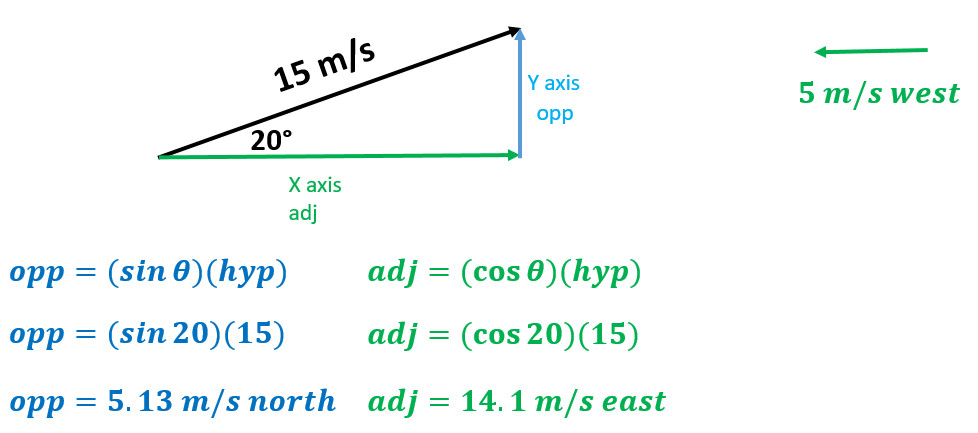
Start by finding the X and Y components of any off axis vector
- Here find the X and Y components of 75 meters 20° North of West

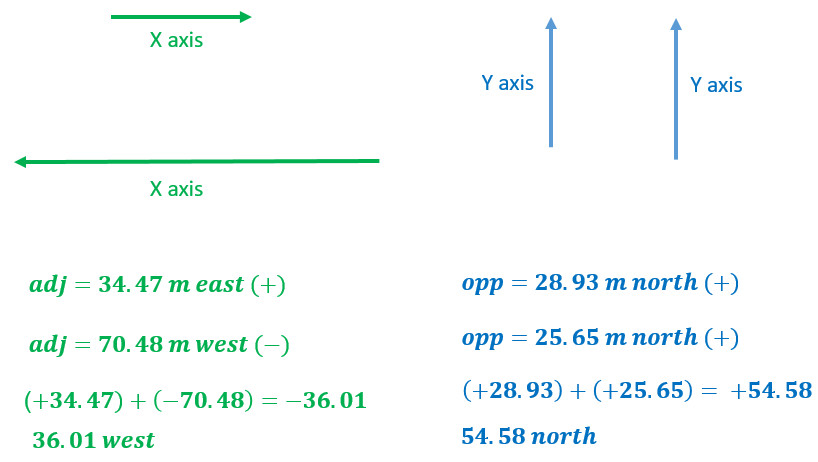
Put any X components together as we did in the 1D motion section
- Here you only will have one X component
Put any Y components together as we did in the 1D motion section
- Here you have two Y components to put together

Now draw an origin dot and the resulting X then Y component
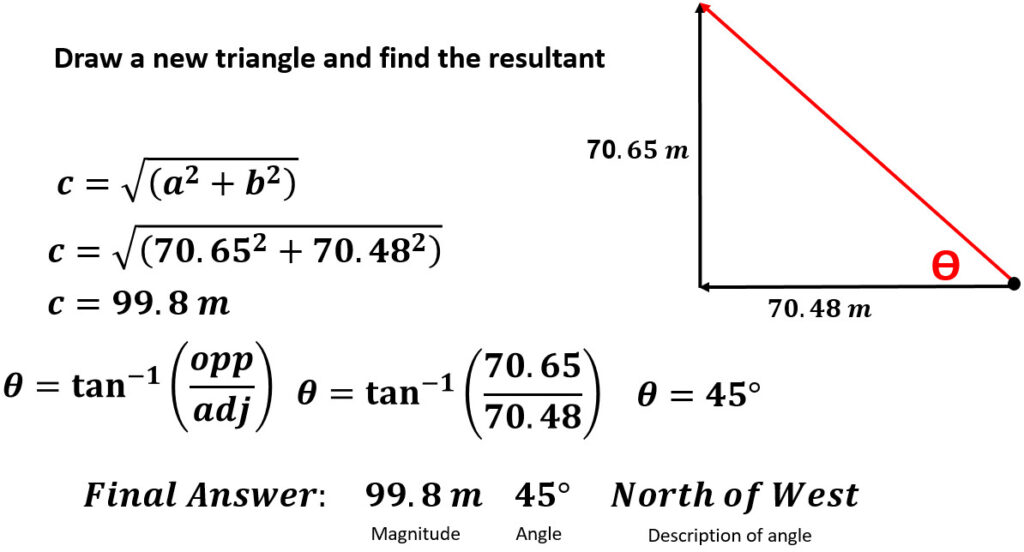
Then draw your resultant from origin to finish
Solve for the resultant magnitude, angle, and description of angle

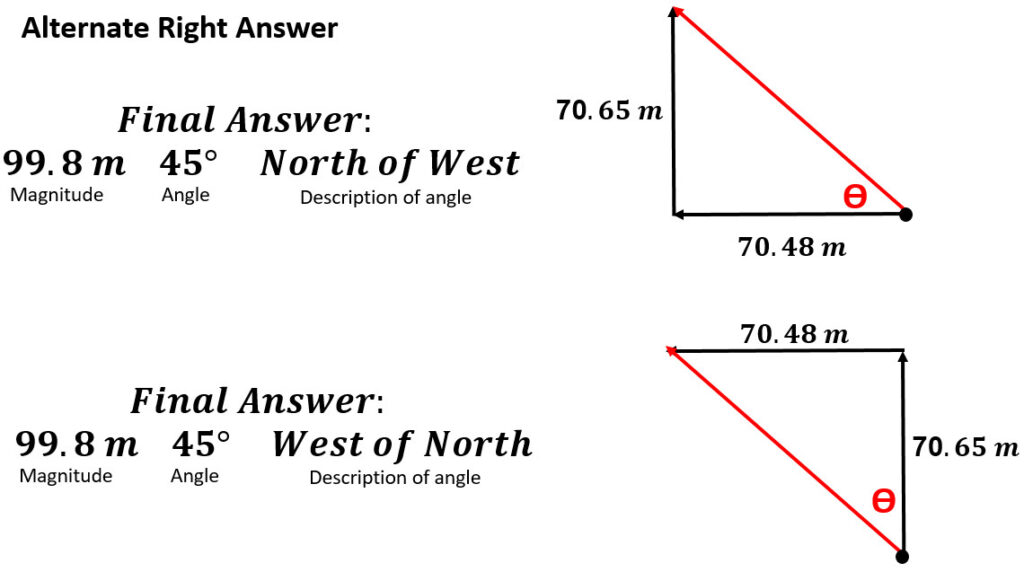
Alternative right answer if you drew the north component before the west

Practice:

Q2: What is the result of boating 15 m/s 20° North of East with a 5 m/s current to the west?

Break down the off axis vector into its X and Y components

Combine all X and Y axis components of all the vectors

Redraw the overall X and overall Y resultant right triangle and solve

Combining Multiple off Axis Vectors to get a Resultant

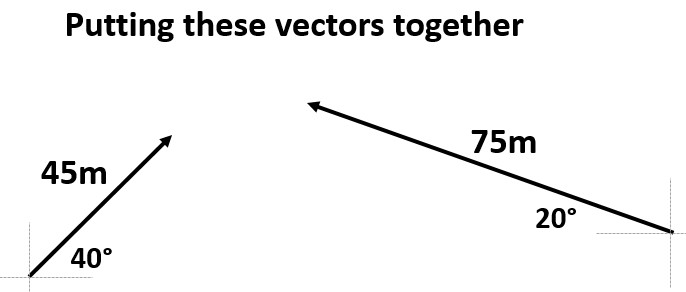
Example: Where is Joe located after traveling 45 meters 40° North of East followed by 75 meters 20° North of West?

Start by finding the X and Y components of any off axis vector
- Here find the X and Y components of 45 meters 40° North of East
- Here find the X and Y components of 75 meters 20° North of West