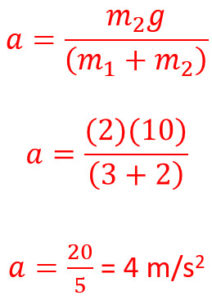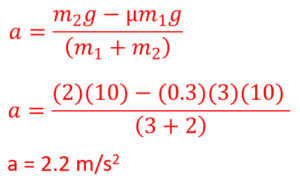Modified Atwood Machines

Home » Modified Atwood Machines

Modified Atwood Machine Physics: solve problems, gain insights, and sharpen skills through examples and practice problems.

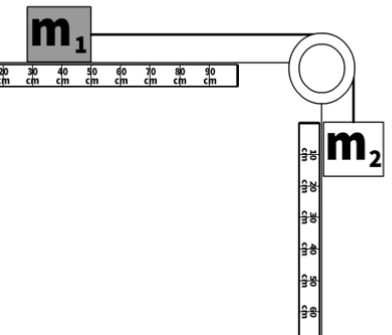
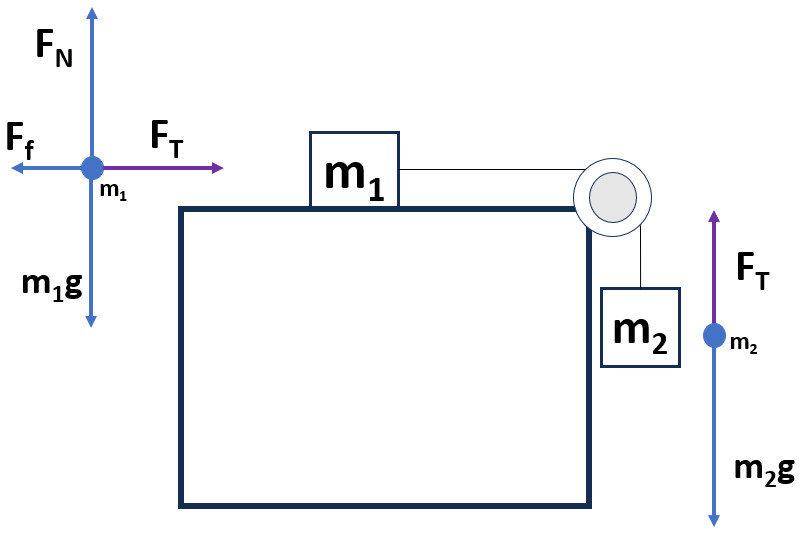
A modified Atwood machine, similar to an Atwood Machine, has a central pulley and hanging masses. Modified because one or more the masses are not hanging and may be on a flat surface or incline.

The pulley changes the direction of the force, and we can use free body diagrams and net force equations to determine a force, net force, and resulting accelerations.

Equal Tension in the Atwood Machine String

The magnitude of rope tension attached to each mass is equal.

Notice in the animation, each block has the same magnitude of acceleration and travel attached to a sting that is moving with the blocks.

Most problems assume a massless rope and pulley and ideal conditions.

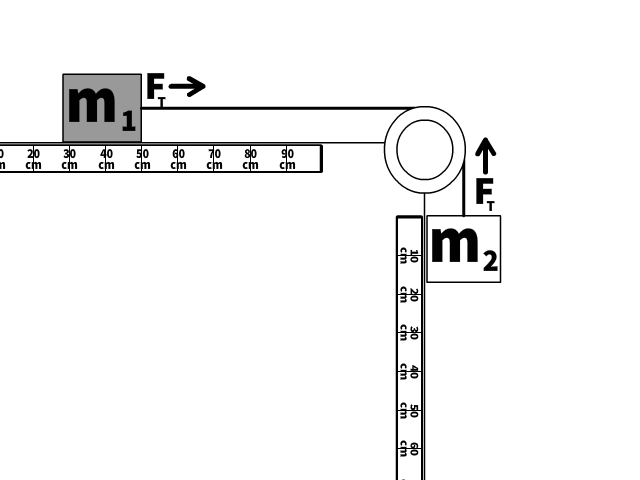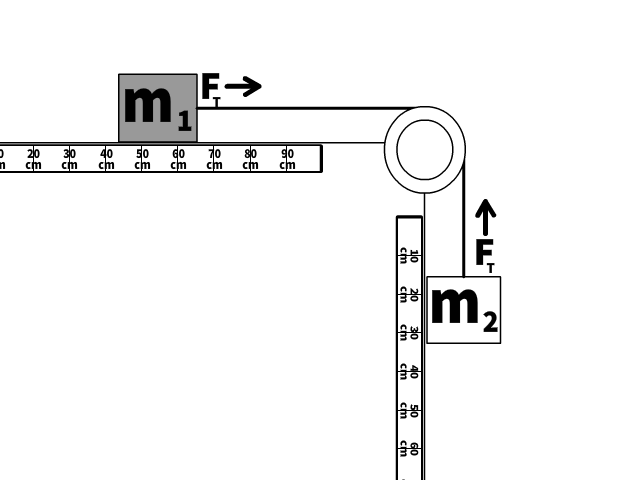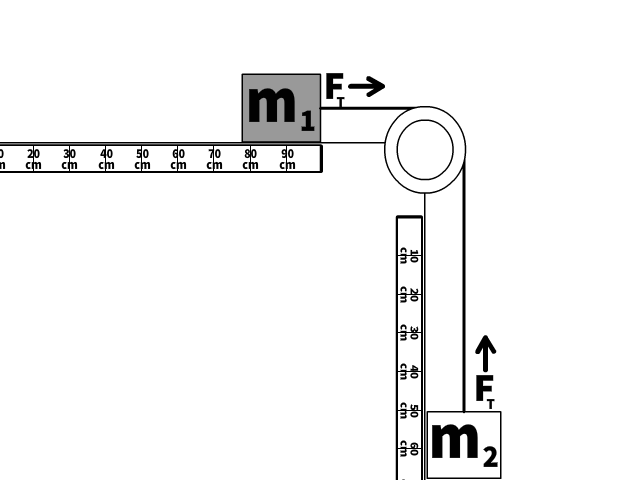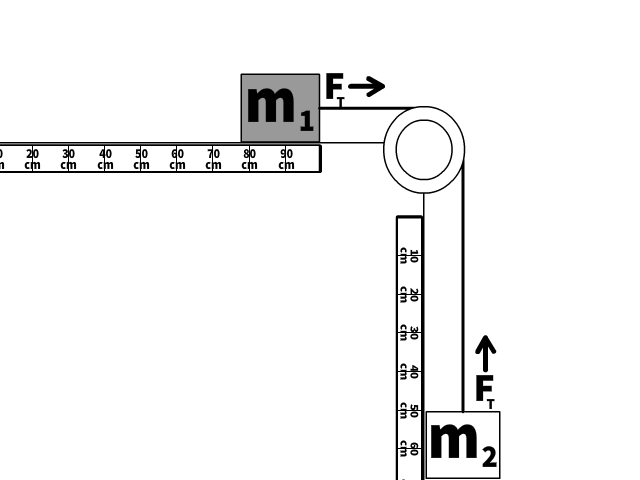
We will look at this scenario two ways:

First, as each block being individual systems

This is necessary to determine the tension in the string
You can use this to solve for acceleration of either block

Secondly, as the two blocks and the massless rope being a system accelerating together

This can be used to quickly solve for the magnitude of acceleration of the system

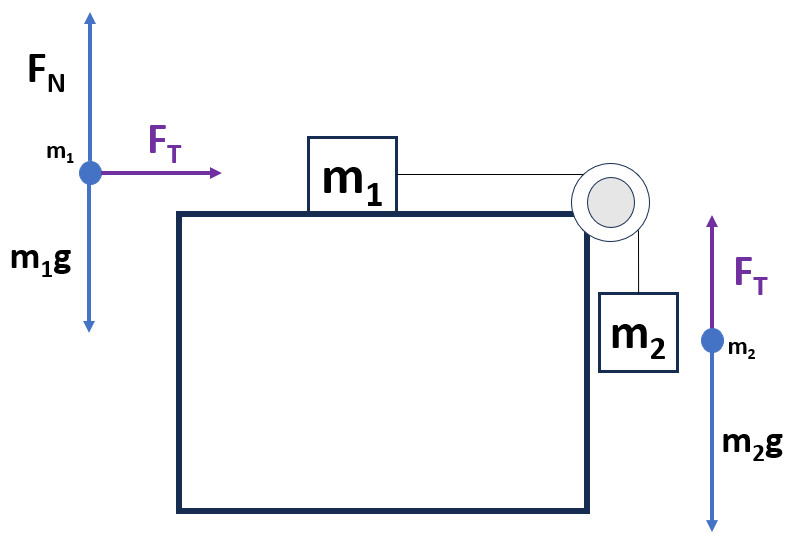
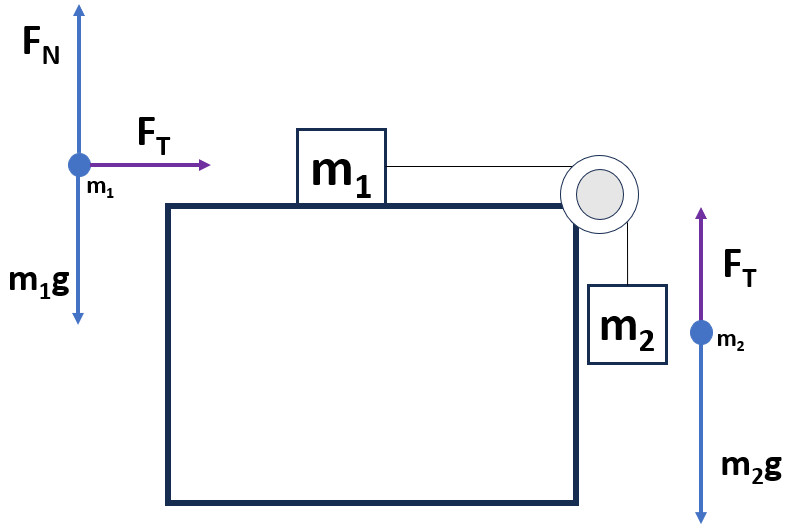
Atwood machine (Blocks Separate Systems)

Block 1 F_net = ma Equation:

Weight (m₁g) and normal force (F_N) are in equilibrium and cancel out.
On a frictionless surface the net force on m₁ would be equal to tension in the string.
Acceleration of m₁ is in the direction of the net force or right here.

Start with Newton's Second Law for mass one.

F_net = m₁a

The sum of force is equal to tension in the rope (right negative).

F_net= ΣF = -F_T

Substitution makes this the Newton's Second Law equation for m₁:

-F_T = m₁a

We can rearrange the m₁ equation for tension.

F_T = -m₁a

m1 Newtons Second Law equation for a modified Atwood machine

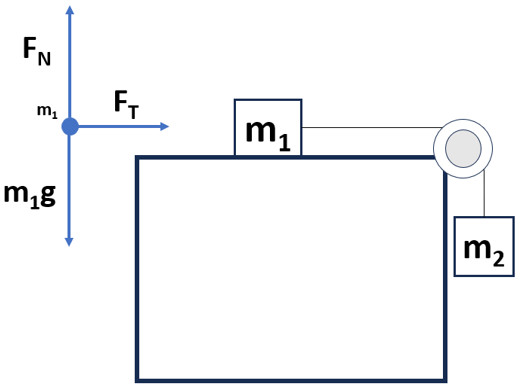
Block 2 F_net = ma Equation:

Sum of forces on m₂: Weight (m₂g) will pull mass two down while tension (F_T) will pull up.
Sum of forces is substituted in for net force creating the m₂ Newton's Second Law equation

Up being positive:

ΣF = F_T – m₂g

F_net = m₂a

Set the net force equation equal to the sum of the forces and substitute.

ΣF = F_net

F_T – m₂g = m₂a

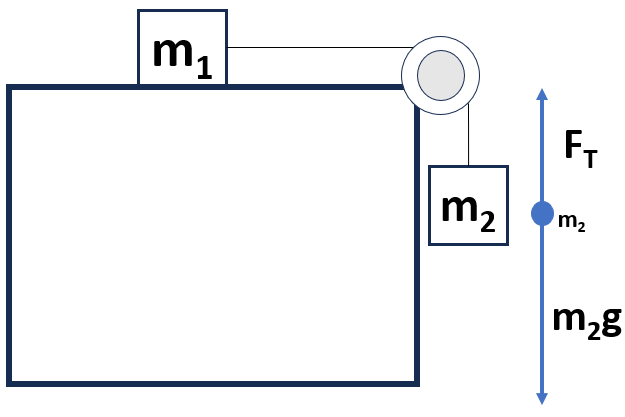
Combining m₁ and m₂ equations to solve for acceleration:

m₁equation:

F_T = -m₁a

m₂equation:

F_T – m₂g = m₂a

Combined after substitution:

-m₁a – m₂g = m₂a

Rearrange for a’s on the same side:

-m₂g = m₁a + m₂a

Factor out common factor a:

-m₂g = a(m₁ + m₂)

Isolate a and place on the left of the equation:

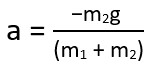
The acceleration of m₁will be to the right and m₂ would be down.

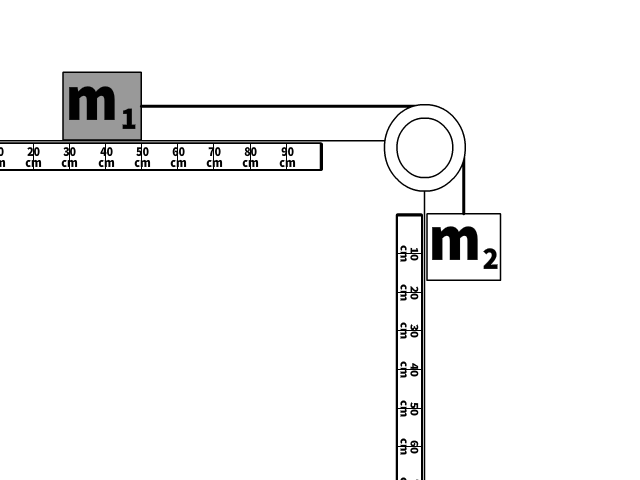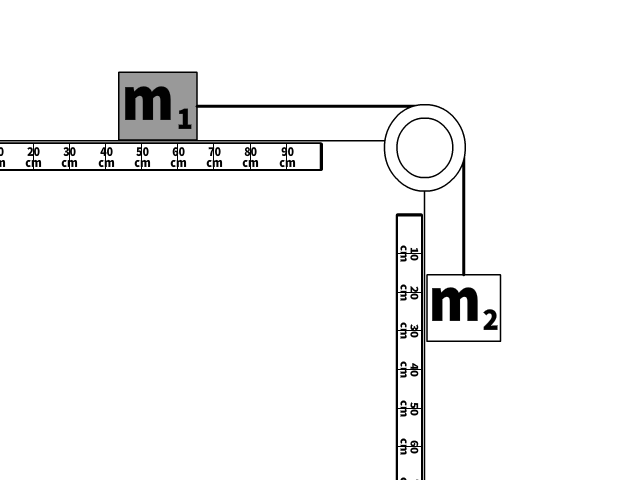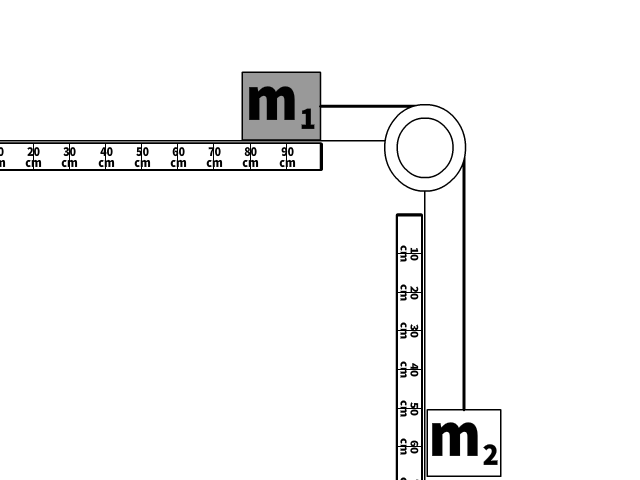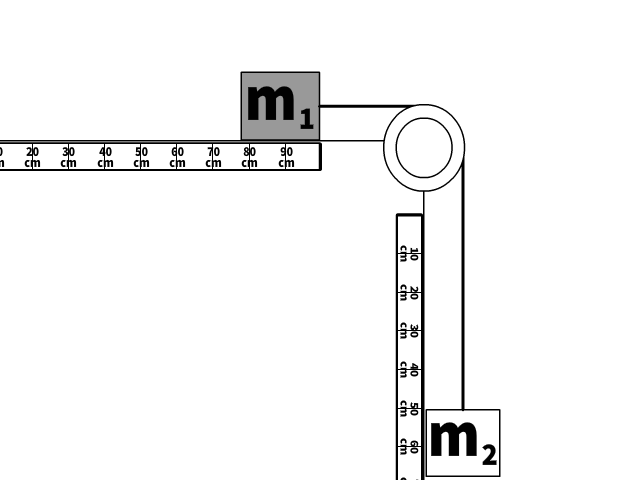
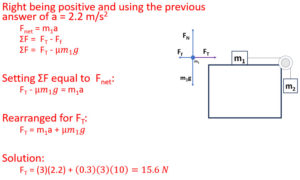
If solving for tension without numerical values

Take acceleration and substitute into the m₁net force equation.

F_T = -m₁a

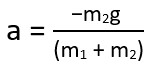
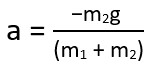
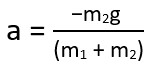
Becomes:

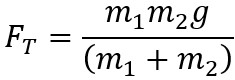
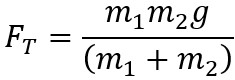
Atwood machine (Blocks with String Combined as a System)

No Friction

Acceleration with no friction starting from the rearranged Newton's Second Law equation

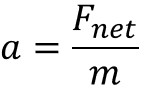
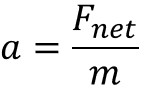
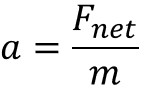
Look at the picture of the scenario.

Tension is internal to the system of m₁ and m₂moving together.
The only force without friction not in equilibrium or internal to the system is the weight of the hanging second mass (m₂g)
m₁ and m₂ accelerate together so m must be replaced by (m₁ + m₂)

The new equation for the acceleration of the system of two blocks:

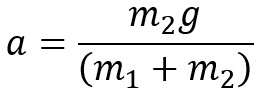
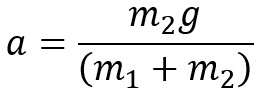
Modified Atwood Example Problem Without Friction:

A) What is the acceleration of 3 kg m₁ if m₂ is 2 kg?

B) What is the tension in the rope between 3 kg m₁ if m₂ is 2 kg?

With Friction

Acceleration with no friction starting from the rearranged Newton's Second Law equation

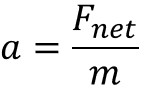
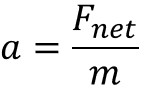
Look at the picture of the scenario.

Tension is still internal to the system of m₁ and m₂moving together.
Now we have the weight of the hanging second mass (m₂g) causing the system to move relative to m₁ rightward and friction will oppose that motion leftward
m₁ and m₂ accelerate together so m must be replaced by (m₁ + m₂)

The new equation for the acceleration of the system of two blocks with friction and right being positive:

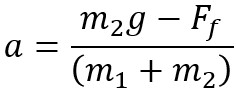
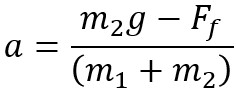
When the force of friction is substituted since F_f = μF_N1
The normal force going into friction would be coming from m₁'s sliding friction

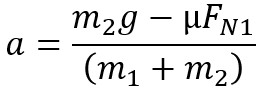
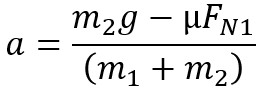
This can be expanded for normal force if on a horizontal surface to become:

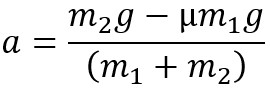
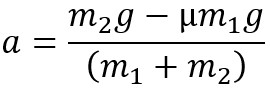
Modified Atwood Example Problem With Friction:

A) What is the acceleration of 3 kg m₁ if m₂ is 2 kg if the coefficient of friction between block m₁ and the surface below is 0.3? (Using 10 m/s² as g)

B) What is the tension in the rope between 3 kg m₁ and 2 kg m₂ if the coefficient of friction between block m₁ and the surface below is 0.3? (Using 10 m/s² as g)