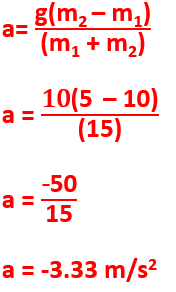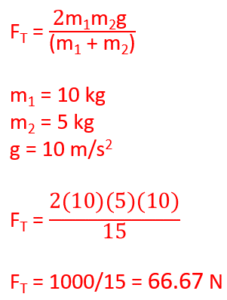Atwood Machines with Two Hanging Masses
Solve problems involving Atwood machines with two hanging masses. Solve for acceleration and tension with variables alone or given masses.
Atwood Machines and Net Forces
Atwood machines are the subject of many AP Physics 1 problems.
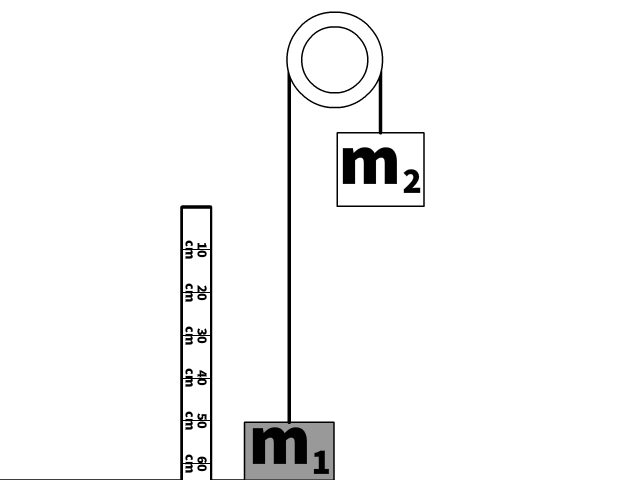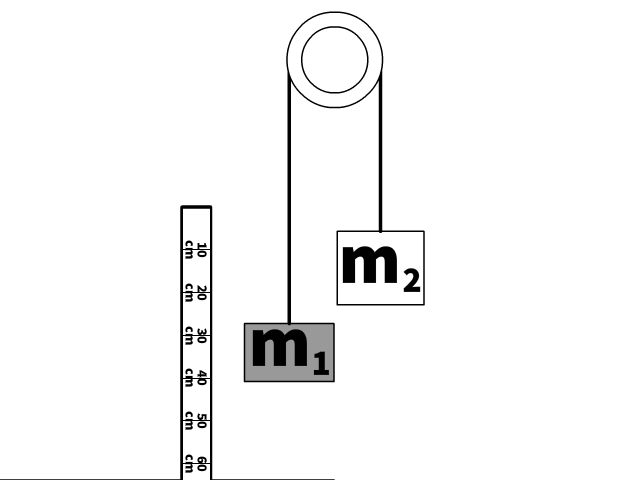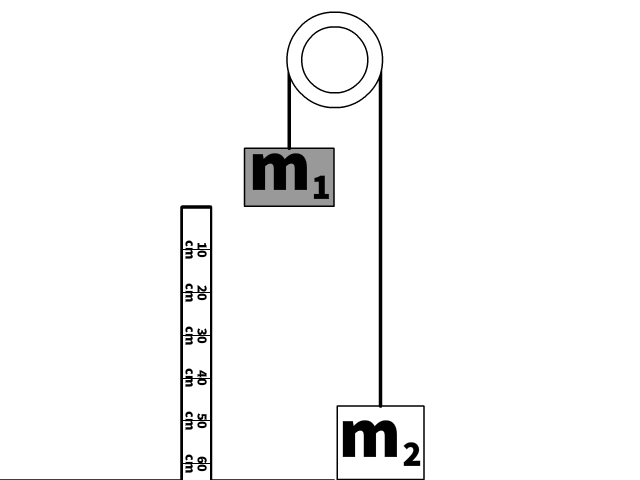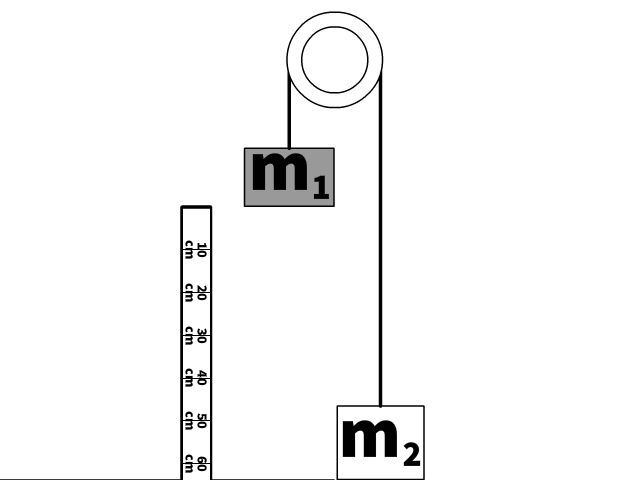
An Atwood machine consists of two blocks hanging from a pulley. The simple pulley with no mechanical advantage changes the direction of the hanging mass force.
The resulting blocks will accelerate if not in equilibrium.
Most problems will assume the pulley and string is massless.
Common Forces in Atwood Machines
It is important to find commonalities so you can create and use mathematical expressions involving multiple objects like mass 1 (m1) and mass 2 (m2) in the animation.
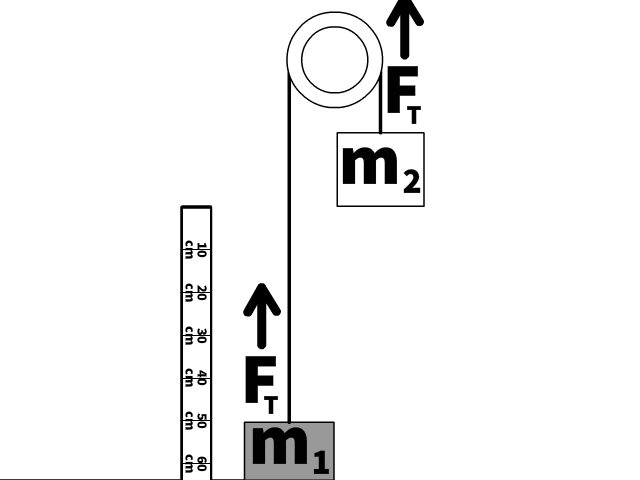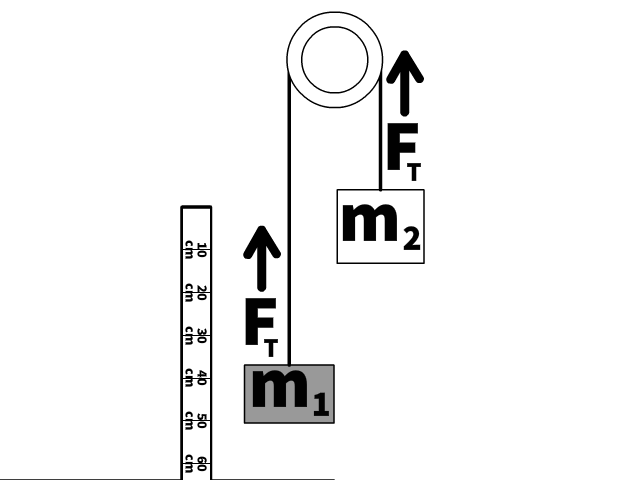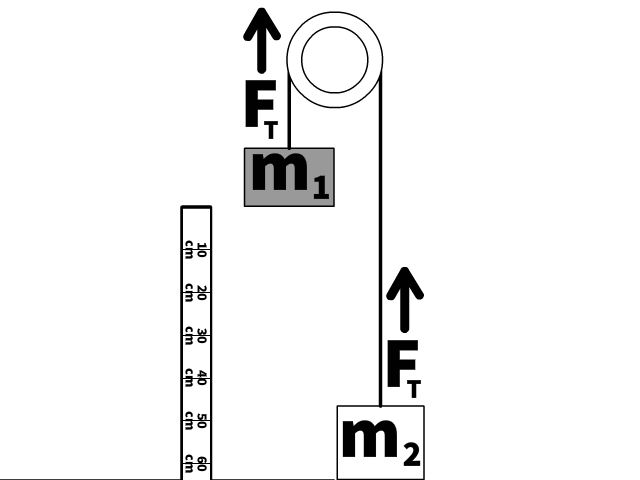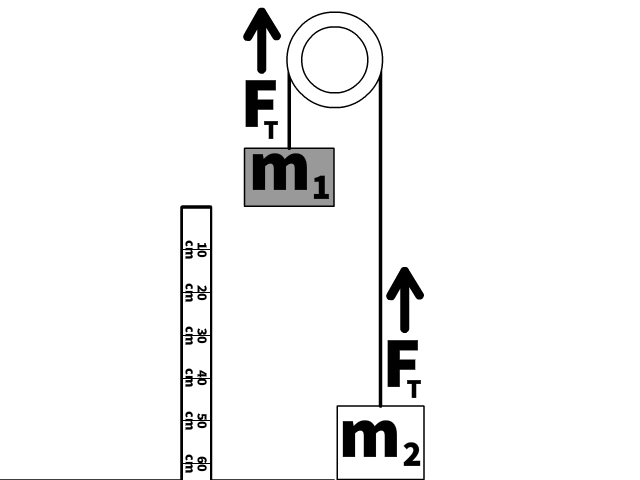
Notice a few facts necessary to understand when solving through Atwood machine problems:
- Masses are attached to the same string.
- Though the direction is different, the masses have the same magnitude of acceleration.
- The side of the string attached to m1, and the other side attached to m2 have the same magnitude of tension (FT).
Determine if the Atwood Machine is in Equilibrium
Masses of an Atwood machine that is in equilibrium (ΣF = 0 N) will be in a state of rest or constant motion.
Masses on an Atwood machine that is not in equilibrium (ΣF ≠ 0 N) will be in a state of acceleration.
Creating an Atwood Machine Equation
Creating Atwood machine Newtons Second Law (Fnet = ma) equations are often used to determine the acceleration of a block or the common tension in the rope between the blocks.
Creating an Atwood Machine Equation in Equilibrium
Creating Atwood machine Newtons Second Law (Fnet = ma) equations are often used to determine the acceleration of a block or the common tension in the rope between the blocks.
An Atwood machine in equilibrium would have equal mass on either side and could be at rest or have the blocks moving at a constant speed.
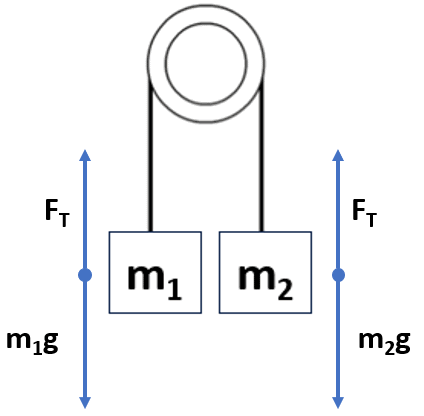
Newton’s Second Law equation (Fnet= ma) of either mass would be similar.
With up being positive:
ΣF = FT – m1g
The net force on each block would have to be 0 (ΣF = 0 N).
0 = FT – m1g
Therefore, when rearranged:
- FT = m1g
And since the solution is the similar:
- FT = m2g
The magnitude of tension in the string is equal to the either mass weight (m1g) or (m2g), only when an Atwood machine with two equal masses hung on each side of a pulley.
Creating an Atwood Machine Equation Not in Equilibrium
When the Atwood machine is not equilibrium (ΣF ≠ 0 N) it is accelerating.
- The magnitude of each block's acceleration will be the same.
- The tension (FT) in the string will be the same.
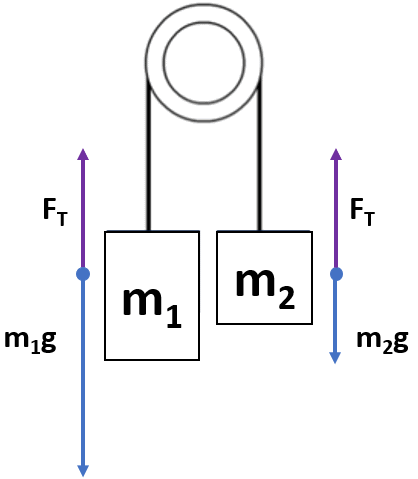
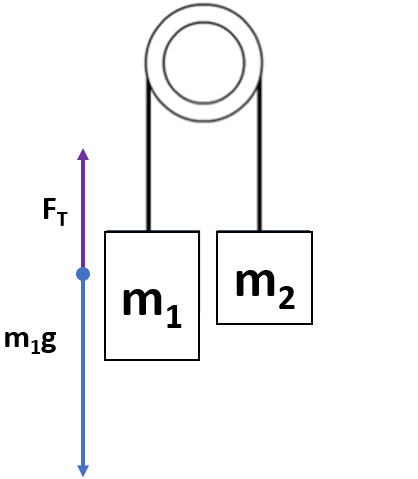
Newton’s Second Law equation (Fnet= ma) of block 1.
With up being positive:
ΣF = FT – m1g
When ΣF is substituted in for Fnet, in Newton’s second law Fnet = ma equation and specialized with m1 and a1, the net force equation for block 1 would be:
FT – m1g = m1a1
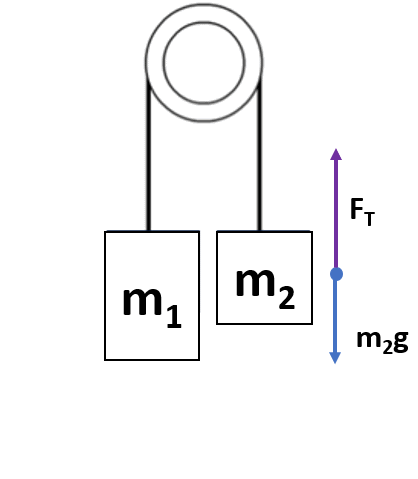
Newton’s Second Law equation (Fnet= ma) of block 2:
With up being positive:
ΣF = FT – m2g
When ΣF is substituted in for Fnet, in Newton’s second law Fnet = ma equation and specialized with m2 and a2, the net force equation for block 2 would be:
FT – m2g = m2a2
Creating Common Variable to use in Substitution
- FT – m1g = m1a1
- FT – m2g = m2a2
Commonalities in these equations:
Tension (FT is the same)
With up being positive
- a1 = +a
- a2 = -a
Substitution of a creates:
- FT – m1g = m1a
- FT – m2g = -m2a
When solving for a
Rearrange the Newton’s Second Law for m1 equation (FT – m1g = m1a) for FT
- FT = m1a + m1g
Substitute the above FT into the (FT – m2g = -m2a)
Newton’s Second Law equation for m2.
m1a + m1g – m2g = -m2a
Rearrange for a:
Step 1: Start by getting a’s on the same side
m1a + m2a = m2g – m1g
Step 2: Then factor out common factors a and g
a(m1 + m2) = g(m2 – m1)
Step 3: Rearrange for an isolated a
![]()
When solving for Tension (FT)
Rearrange the Newton’s Second Law for m1 equation (FT – m1g = m1a) for a
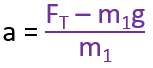
Substitute the above a into the (FT – m2g = -m2a)
Newton’s Second Law equation for m2.
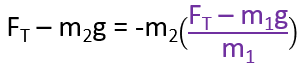
Take steps to get FT on both sides and isolate FT:
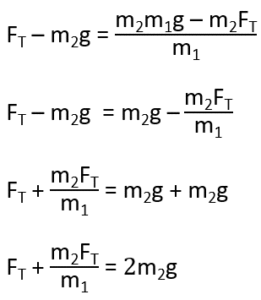
Multiply both sides by m1
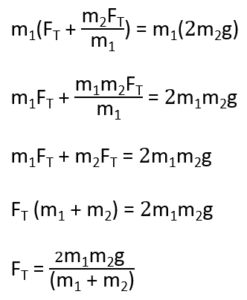
Q1) What is the acceleration of an Atwood machine that has a 10 kg hanging mass on the left and 5 kg hanging mass on the right side of the pulley?
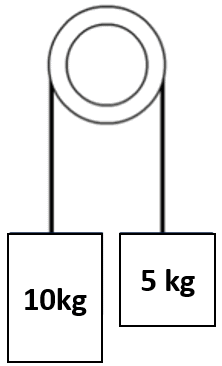
Q2) What is the tension in the string of an Atwood machine that has a 10 kg hanging mass on the left and 5 kg hanging mass on the right side of the pulley?



Lets solve the same problem with the derived equation to check our work:
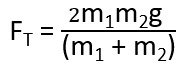
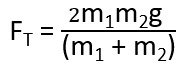
The results are hidden until you click below:
Links
- Forward: Modified Atwood Machines
- Back to Weight Normal Force and Tension (Single Block)
- Back to the Main Forces Page
- Back to the Stickman Physics Home Page