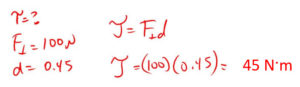Torque
Torque creates rotational acceleration when a force is applied to a lever. Follow examples on this StickMan Physics page.
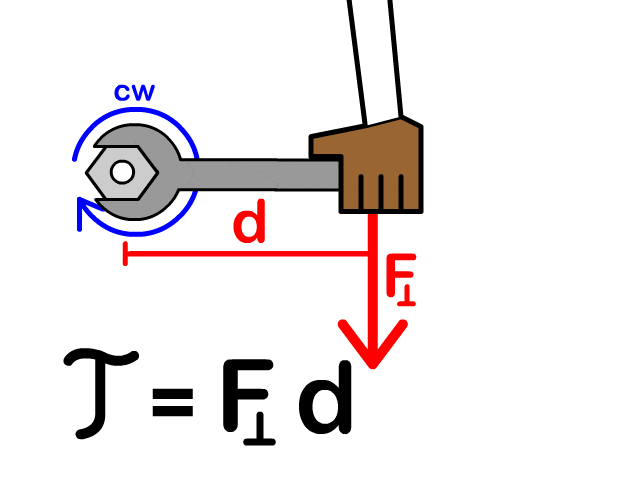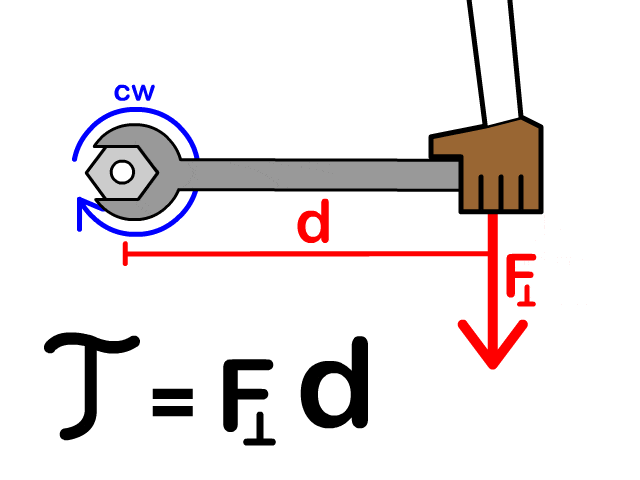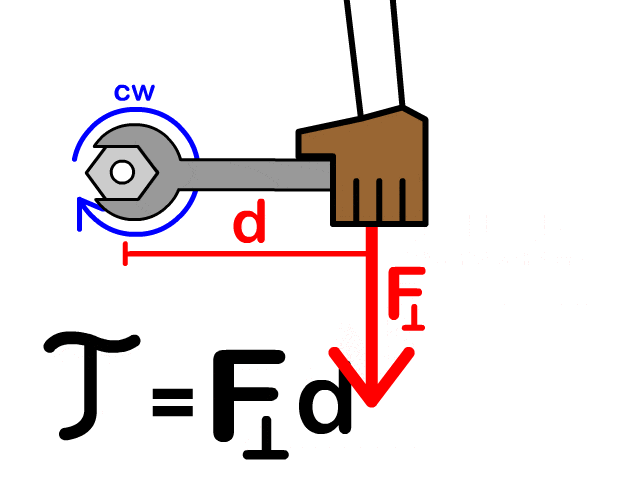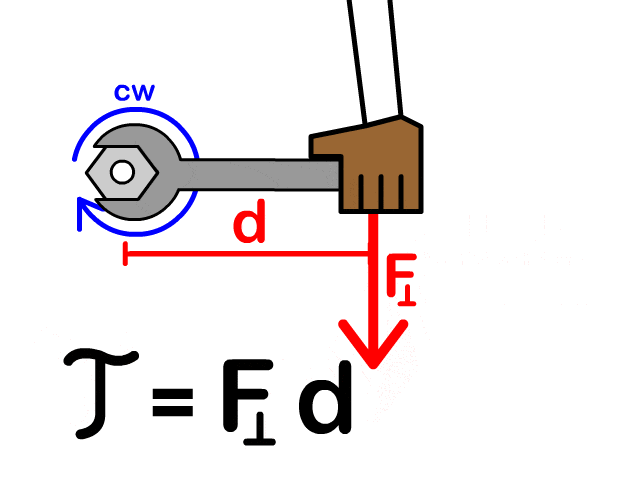
Torque (τ) is the rotational equivalent of force and creates a rotational acceleration. Therefore torque occurs around a fulcrum or pivot point which is the center of rotation. A triangle can represent the fulcrum with a rotation either clockwise (CW) or counterclockwise (CCW). Clockwise is the direction a clocks handle rotates and can be seen in the picture.
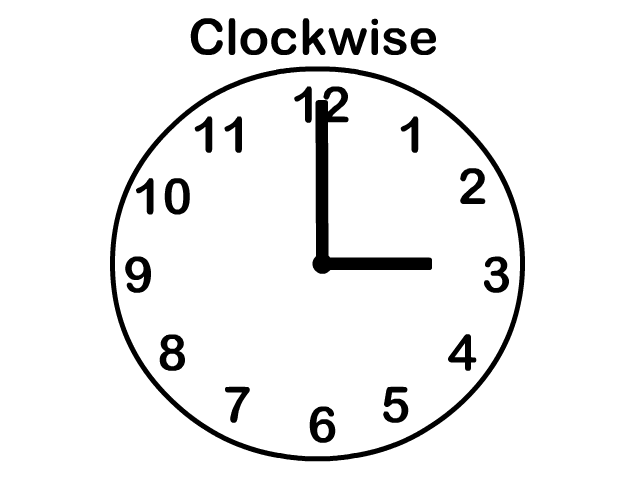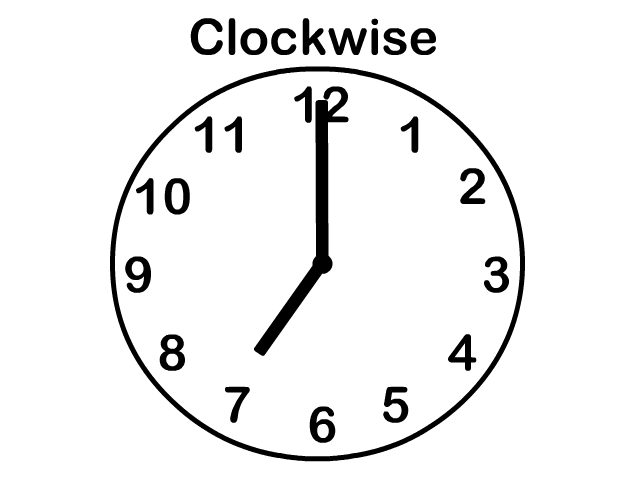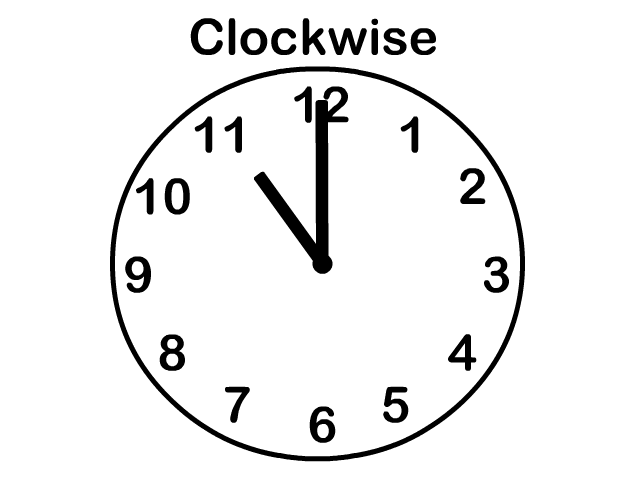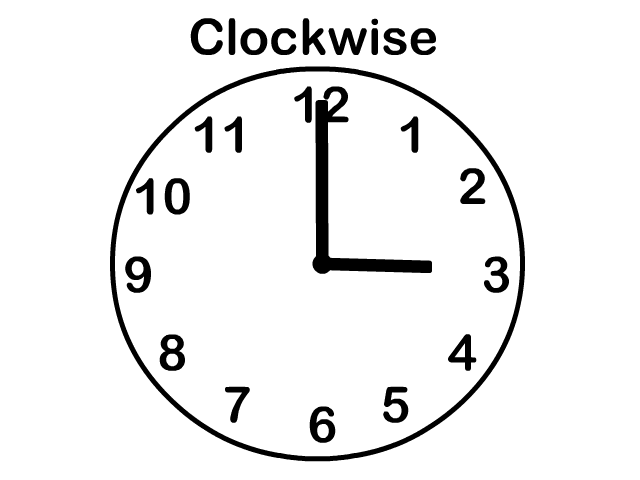
Torque occurs when you apply a force with a perpendicular component to a lever or length away from a rotating point. See torque equation variables and standard units below.
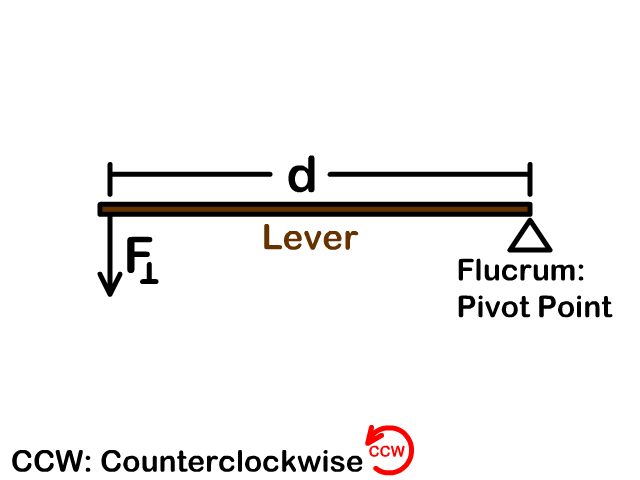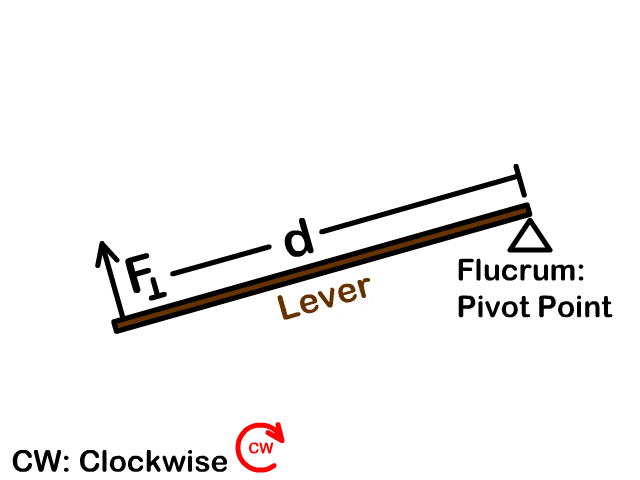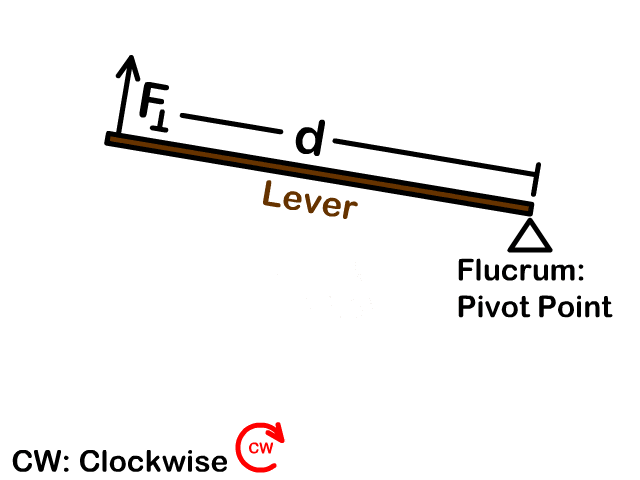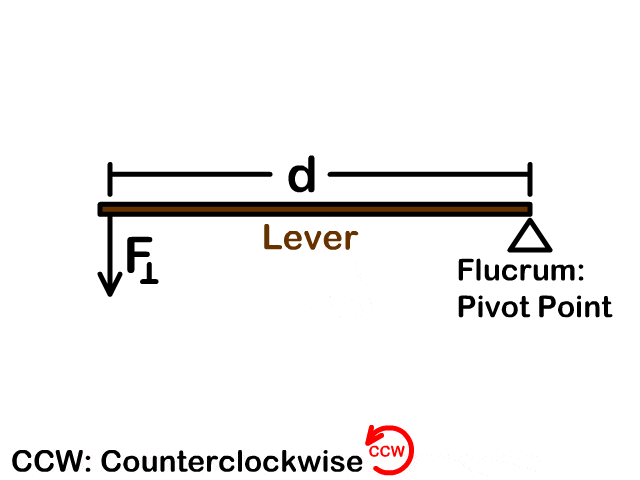
Torque Variables
| Name | Variable | Unit | Unit Abbreviation |
| Torque | Ƭ | Newton times meter | N∙m |
| Perpendicular Force | F⟘ | Newton | N |
| Distance | d | Meters | m |
Torque Equation (τ =F⟘d)
Torque increases as distance away from the fulcrum a perpendicular force is applied. It also increased when the force itself increases. So perpendicular force and distance directly relate to torque. Therefore, an increase either perpendicular force or distance torque, keeping everything else the same, torque would go up.
Example Problems:
Q1: How much torque do you create with a 100 N perpendicular force placed 0.45 meters from the fulcrum?
Q2: How much force would Joe have to apply perpendicular to create 550 Nm of torque 0.20 meters away from the bolt he is trying to loosen?
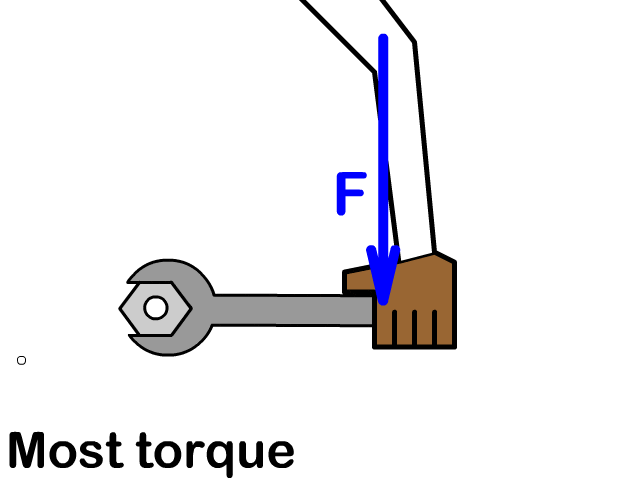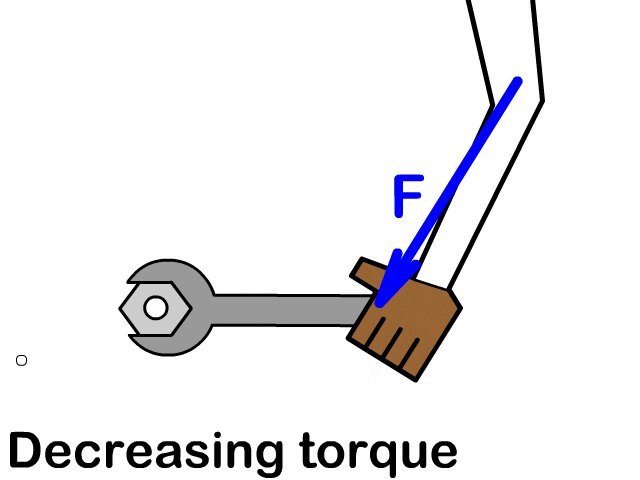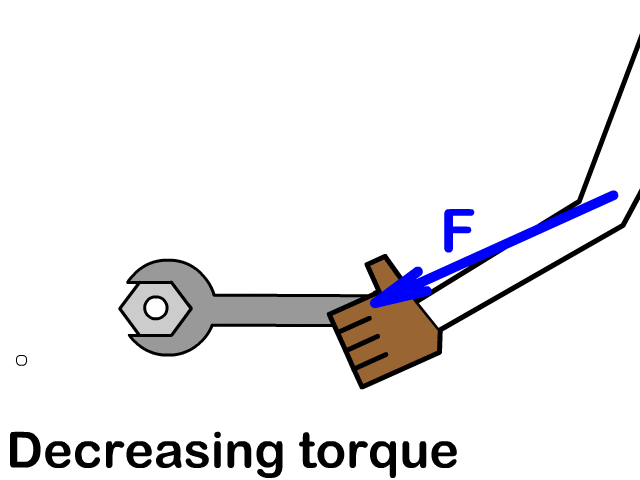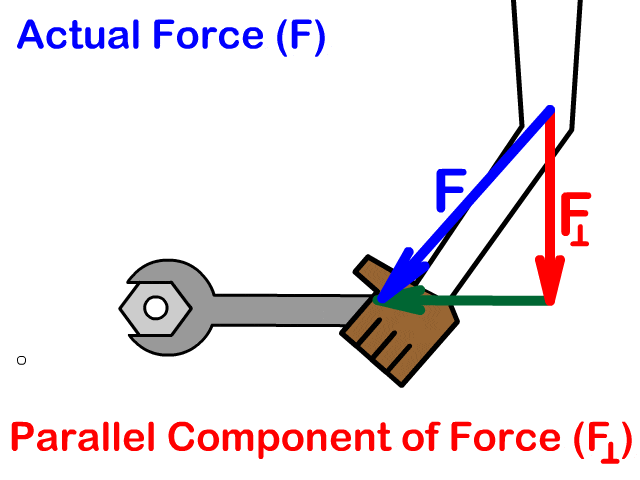
Perpendicular Force Gives the Most Torque and Parallel None
Any force other than one applied parallel can have a perpendicular component seen by the red arrow in the animation. The blue arrow is the actual force applied and the green arrow is the wasted parallel component of force that does not create torque. Torque decreases as force at an angle away from the perpendicular direction increases. 90 degrees is the furthest away from the perpendicular and would be parallel. Therefore, you produce no torque when force is parallel.
Example Problems:
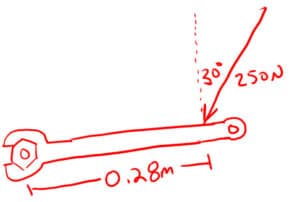
Q3: What torque results from a 250 N force 30° from perpendicular on a wrench 0.28 meters away from the bolt?
Multiple Torques
You add multiple torques after accounting for direction. Any clockwise force will be positive mathematically and counterclockwise negative.
Balanced Systems
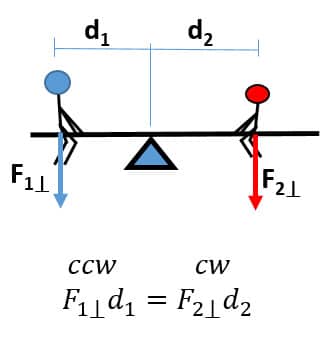
When you have a balanced system, for example, two kids on a teeter-totter, the sum of the forces is equal to zero. You can rewrite the equation with all of the counterclockwise (CCW) forces written on the left of the equals and all the clockwise forces written on the right. Since all the counterclockwise forces will be negative on the right side of the equation, they will be positive when added to both sides. The result is the bottom balanced torques equation (… + F1⟘ d1⟘ = F2⟘ d2 + …). When more torques are in a system, you add them to their corresponding clockwise or counterclockwise side and renumber.
Standard Balancing Torques Equation
In the picture, there are two stickmen on a teeter-totter. The blue stickman on the left creates a counterclockwise (CCW) rotation and the red on the right creates a clockwise (CW) one. They balance each other (zero sum of torques) resulting in the equation below them (F1⟘ d1 = F2⟘d2). If there was an additional person on the left (counterclockwise torque) this would become (F1⟘ d1⟘ + F2⟘ d2 = F3⟘d3). If there was an additional person on the right "instead" it would become (F1⟘ d1 = F2⟘d2 + F3⟘d3). The … in the equations above mean you add as many individual distances and forces to that rotational side.
Example Problem
Q4: How far away on the other side of a teeter-totter must 80 kg joe sit than Mary who is 40 kg when she is 1 meter away from the fulcrum?
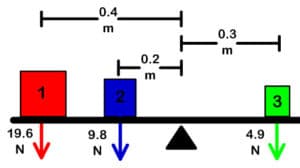
Q5: What is the sum of all torques in the system above?
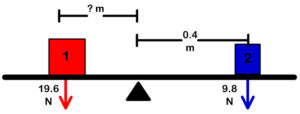
Q6: Where should you place a 19.6 N weight to balance a 9.8 N weight 0.4 meters on the right?
Torque Practice Quiz
- Go to the main Universal Gravitation and Circular Motion Page
- Back to the Stickman Physics Home Page
- Equation Sheet