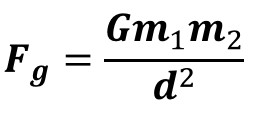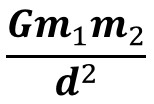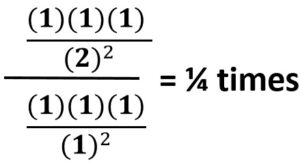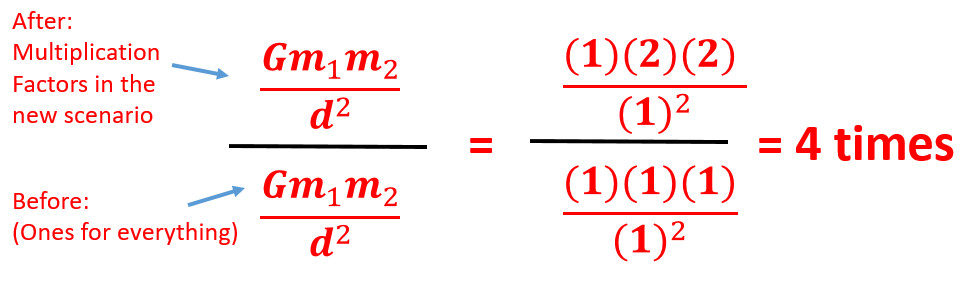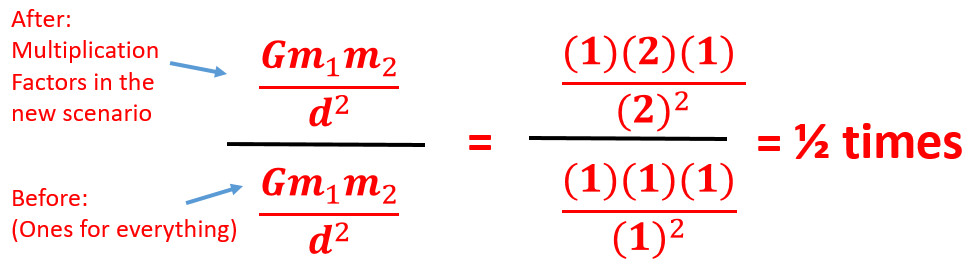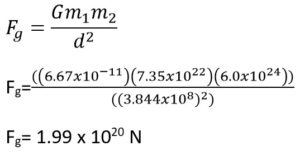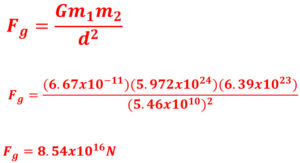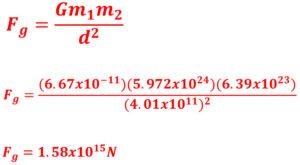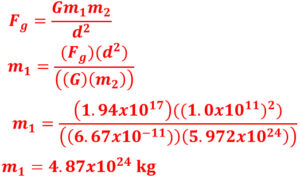Gravity and the Universal Gravitation Equation
Learn how to use Newton's Law of Universal Gravitation. The force of gravity a weak force resulting from two objects having mass and the distance between them. Universal gravitation is not just planetary but attracts you to everything around you as well.
Isaac Newton's Big Idea
Isaac Newton had a lot of brilliant ideas in his lifetime and a massive one was universal gravitation. Universal gravitation is not just the fact that objects on earth fall to the ground. His big idea was that all objects in the universe attract all other objects. An apple may or may not have hit him in the head to cause this revelation. While the apple is probably not true it's not far from the point. Isaac Newton questioned two things. Why would object on earth fall to the ground while the moon continued in its circular path?

The Moon and Apple Both Fall
Newton realized that both the apple and moon are really falling. The earth follows the rules of the rest of the universe. The apple is starting from rest and being attracted to the ground. The moon has inertia, which normally would make it continue forward at a constant velocity but the attraction to the Earth makes it fall.
The moon acts like a projectile with its inertia taking it forward as it also falls to the earth. This combined action keeps the moon in orbit around the earth.

Q1: What was Isaac Newton’s big idea related to gravity?
Q2: Why does the Moon’s not collide with the Earth if there is an attraction?
Newton's Law of Universal Gravitation Equation
Any object with mass (m1) is attracted to any other object with mass (m2).
- This is universal as the name says meaning "all" objects which have mass.
The amount of force depends on distance (d) and related by the universal gravitation constant (G).
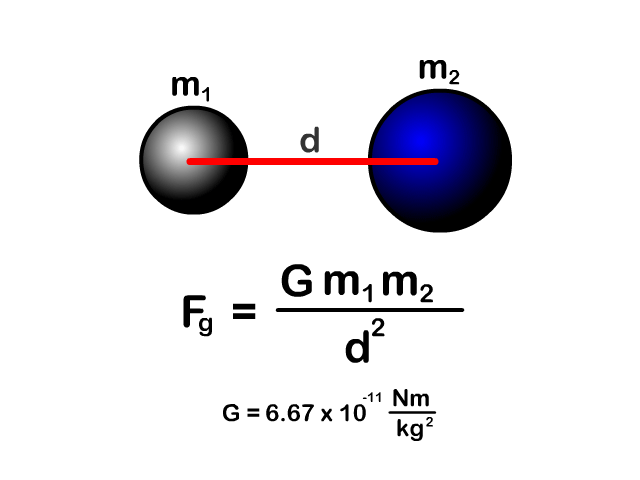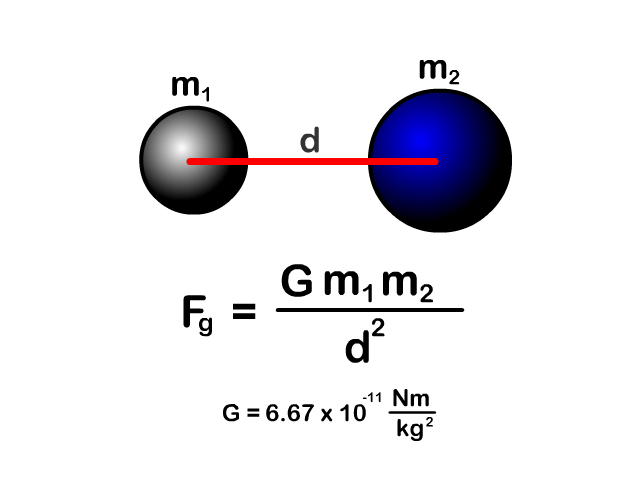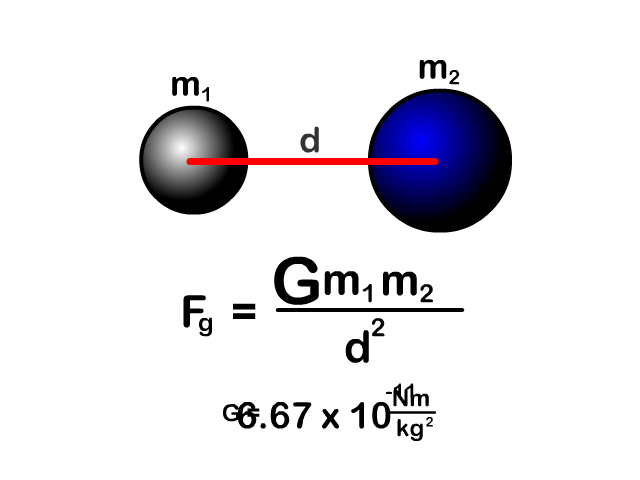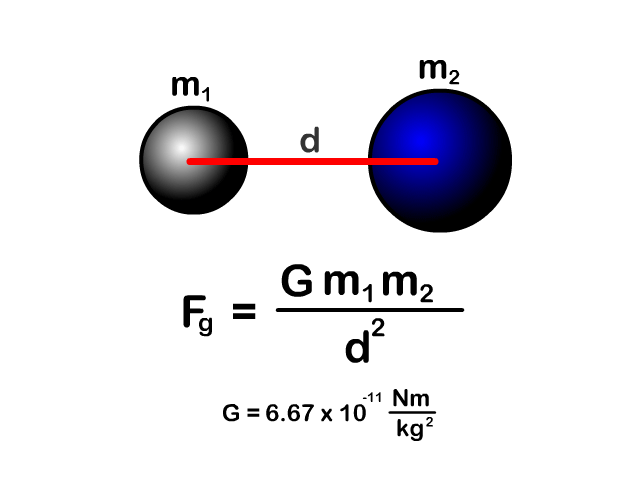
| Variable | Name | Unit | Unit abbreviation |
| Fg | Force of gravity | Newton | N |
| m1 | Mass of one object | kilograms | kg |
| m2 | Mass of a second object | kilograms | kg |
| d | Distance between the objects | meters | m |
| G | Universal Gravitation constant | Newton∙meters/kilograms squared | Nm2/kg2 |
| g | Acceleration due to gravity | Meters per second squared | m/s2 |

Universal Gravitation Constant (G)
The universal gravitation constant (G) is a very small number 6.67 x 10-11 Nm2/kg2 and not the 10 m/s2 (g) for the acceleration due to gravity when objects are on earth.
- Universal gravity is the weakest of the fundamental forces in the universe.
- Because gravity is such a weak force, gravity takes massive objects like the earth (5.972 × 1024 kg or 5,972,000,000,000,000,000,000,000 kg) to feel it.
You feel the earth’s attraction, your weight (FW), but no other object “also” attracting you in a room.
The weakness can be seen by the gravitation constant (G) being so small. 6.67 x 10-11 is a really small number 0.0000000000667.
Weight and Force of Gravity
You attract the earth with a force equal to that which the earth attracts you.
Weight (Fw) is equal to the force of gravity (Fg)
- Using your mass (m1)
- Earth’s mass (m2)
- The distance between you and the center of the Earth (d) (Earth’s radius)
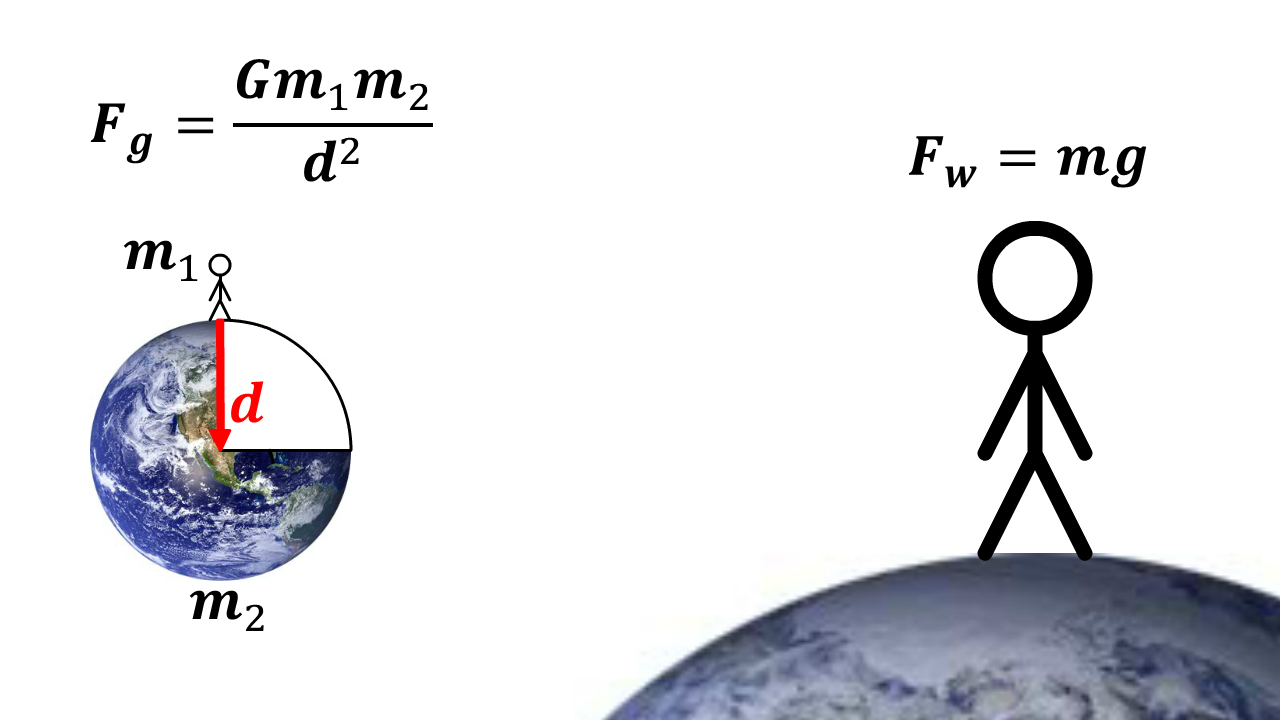
Analyzing the Universal Gravitation Equation
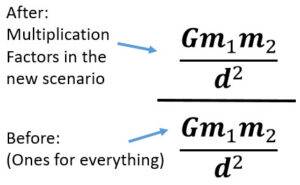
One way to analyze the force of gravity equation, place a 1 in for everything representing no changes. Then change the one thing you are trying to analyze to a bigger number 2 and see what happens. The rule of ones (click here) is a more detailed way to see how multiple changes alter force.
How do you answer a question like this:
How does the force of gravity change when you double the distance between two objects?
You set up a ratio following the steps below:
1. First find the equation most related. This question asks about force when you are changing distance between.
2. Then find what you are trying to analyzes equivalent.
3. Then create ration of after (top) vs. before (bottom)
4. Plug in ones for everything that did not change. This is the same as saying it is one times itself or in other words, itself.
Once you solved for this you know the ratio of how many times different the force now is compared to the original.
5. If you knew the original value, you would multiply it by this ratio.
Q3: What happens to the force of gravity when you double the mass of both objects?
Q4: What happens to the force of gravity if you double the mass of one object and double the distance between objects?
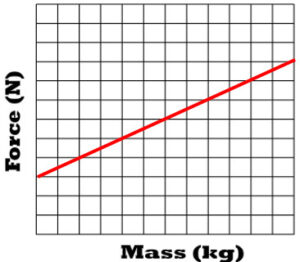
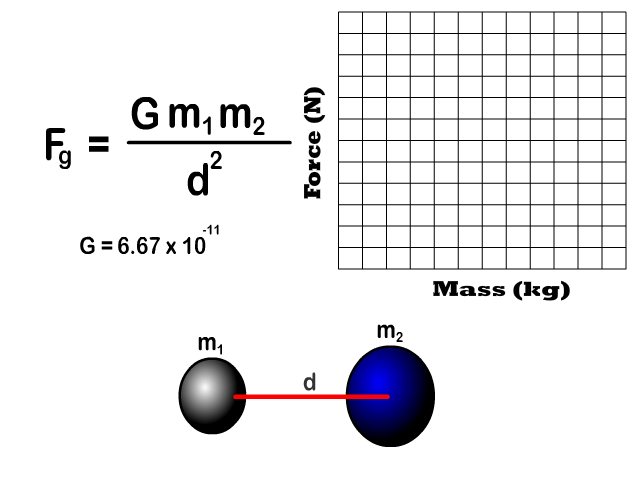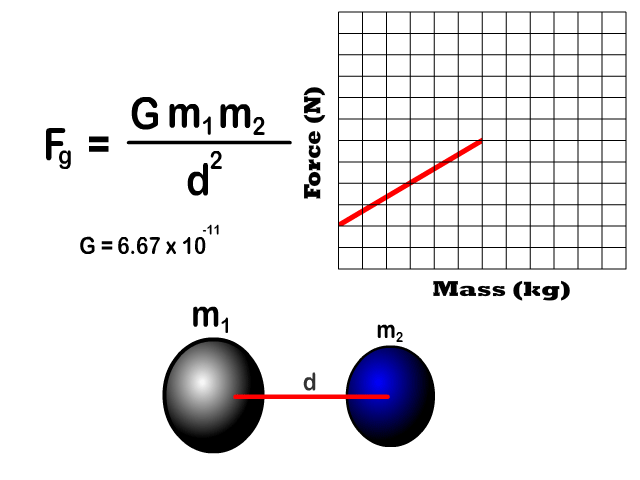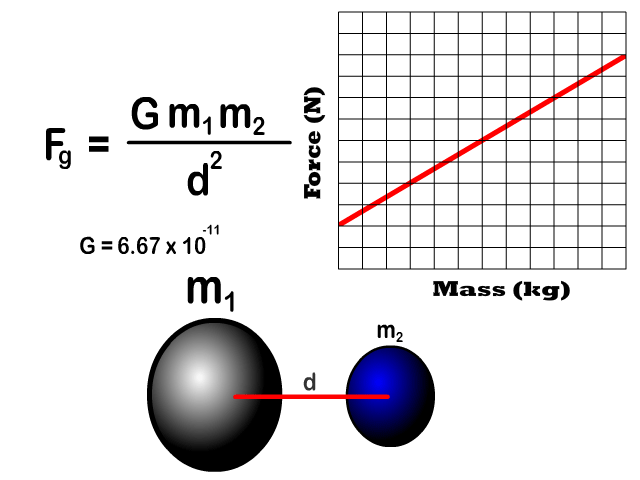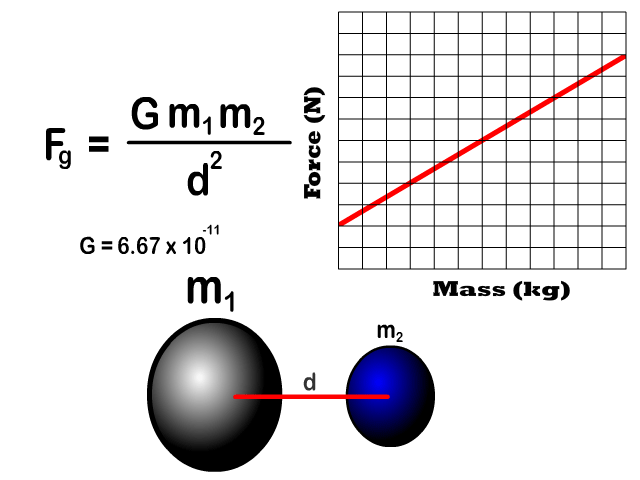
Force of Gravity Relative to Mass
- Gravitational force is directly proportional to mass of an individual object
Q5: Draw the shape of the graph of increasing mass of one object to the force of gravity
Q6: If the mass of one object increases what happens to the force of gravity and at what rate?
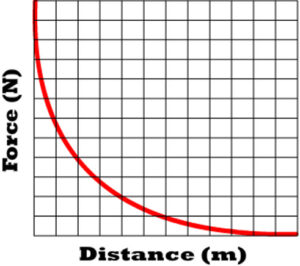
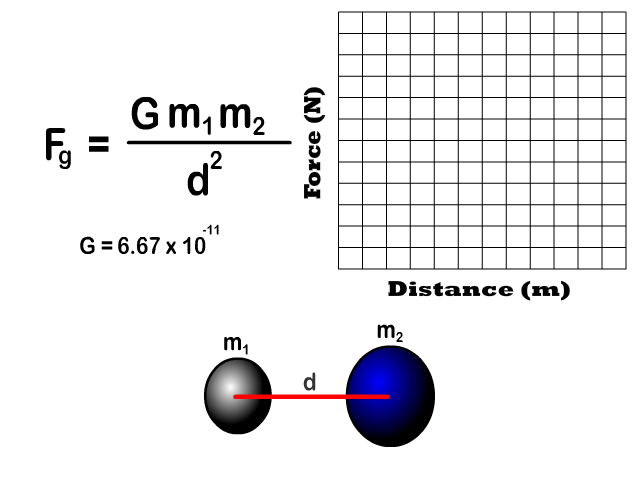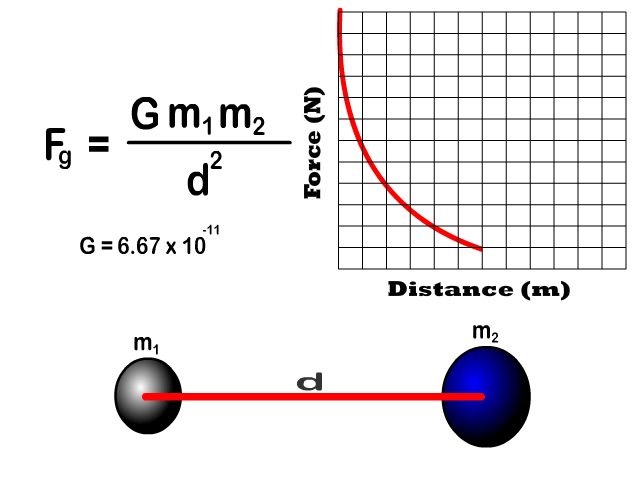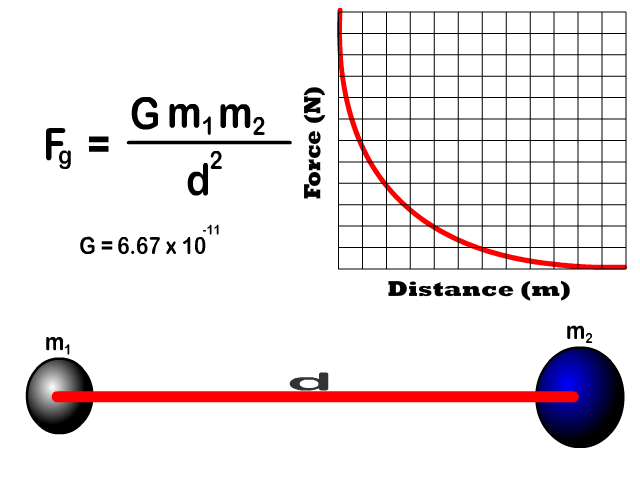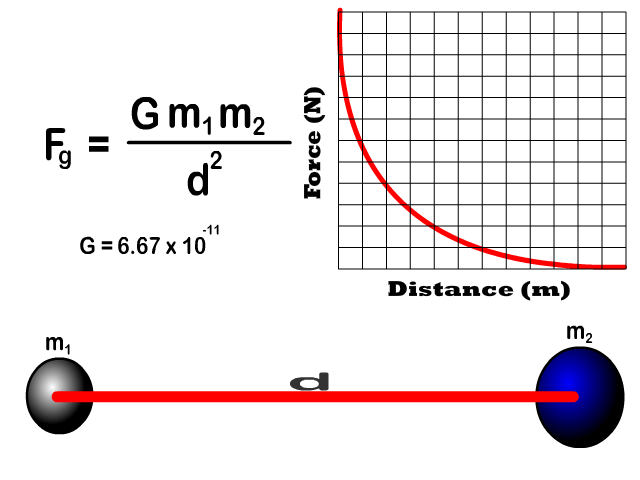
Force of Gravity Relative to Distance
- Gravitational force between two objects is inversely proportional to the square of the distances (inverse squared).
Q7: Draw the shape of the graph of increasing distance to the force of gravity
Q8: If the distance between two objects increases, what happens to the force of gravity and at what rate?
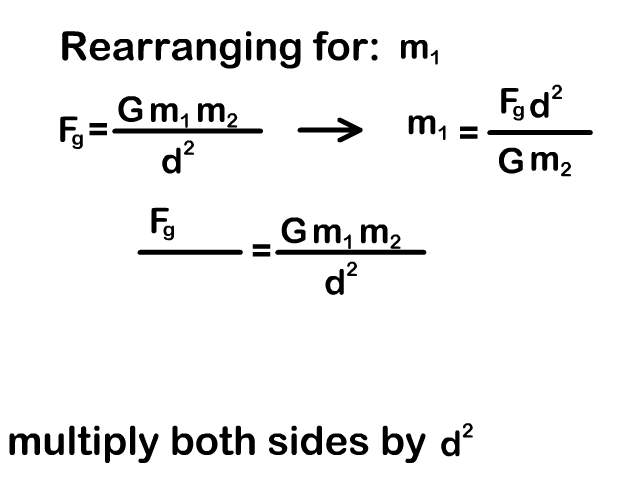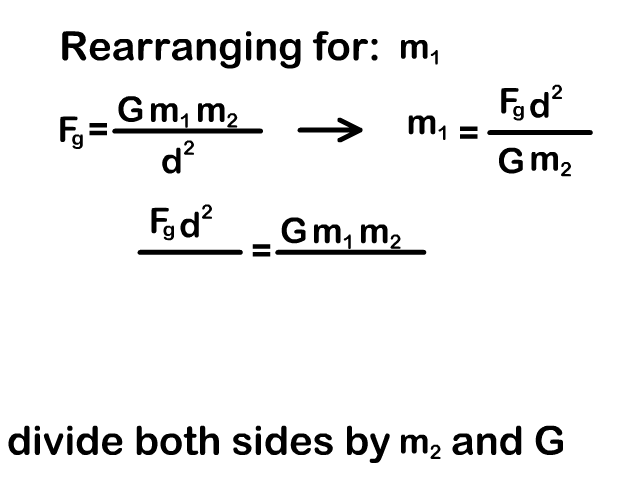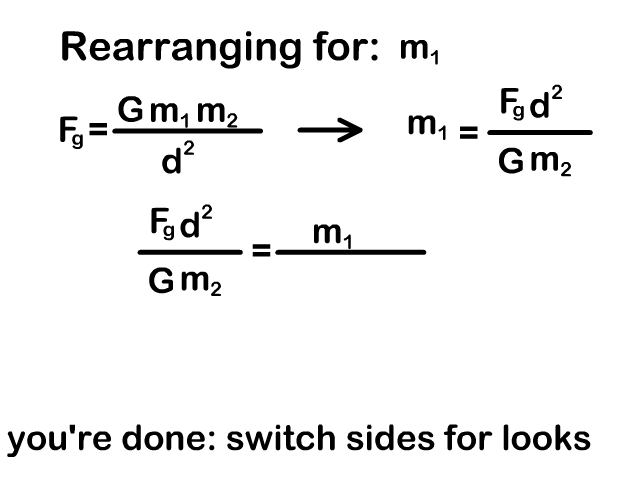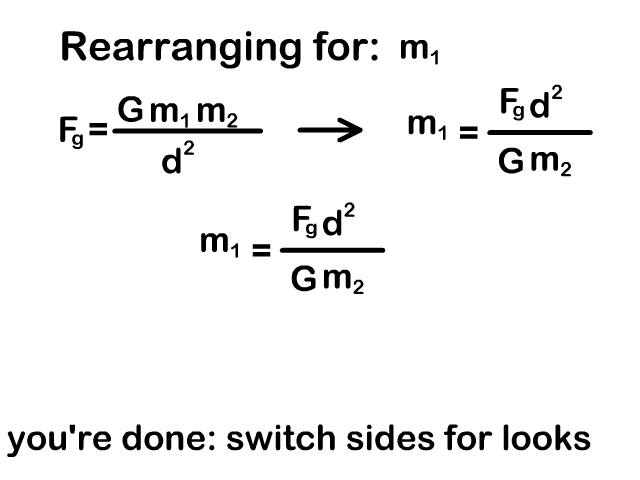
Rearrange the Universal Gravitation Equation
You need to be able to rearrange the universal gravity equation to solve for a mass or distance between objects. Our animations on the right show the process.
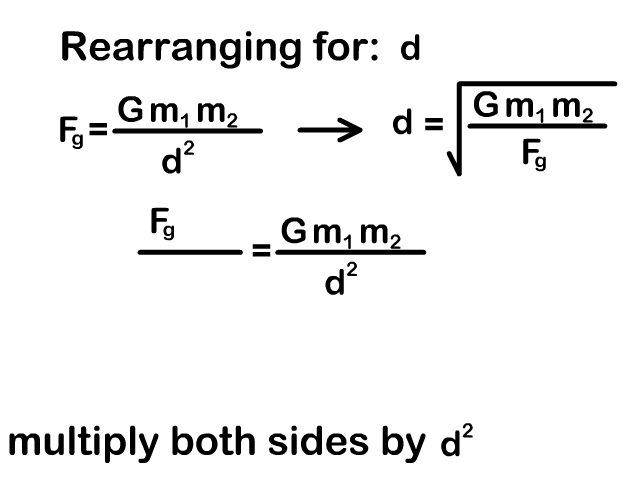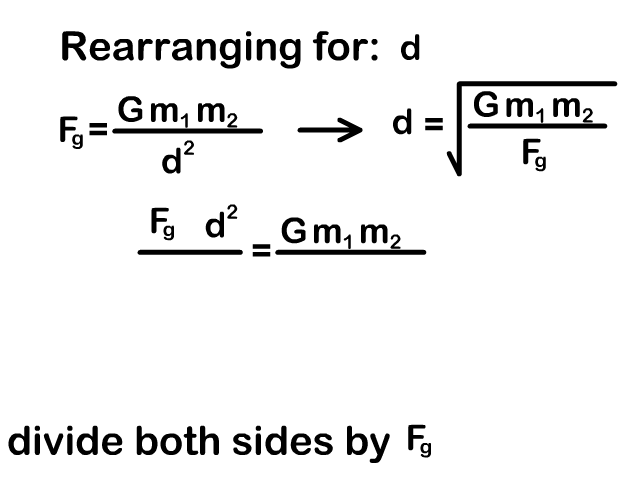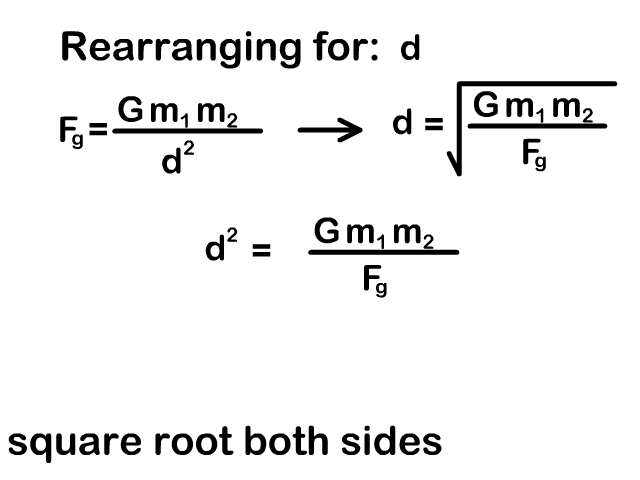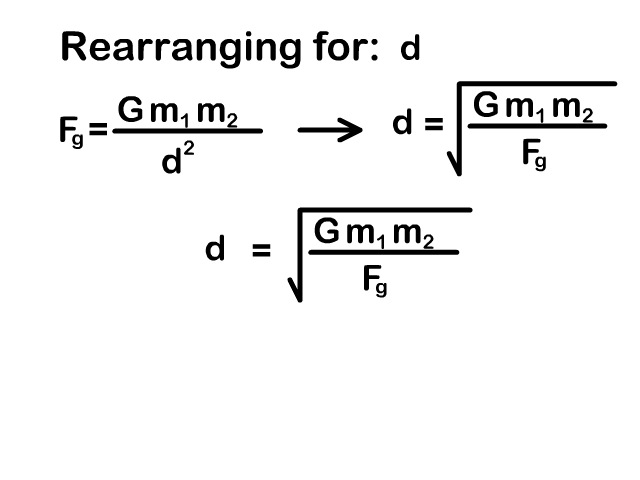
Example Problems:
Q8: What is the force of gravity between the Earth (mearth = 6.0x1024 kg) and the Moon (mmoon = 7.35x1022 kg) when they are 3.844x108 m apart?
Q9: What is the force of gravity between Earth (5.972 × 1024 kg) and Mars (6.39 × 1023 kg) when they are at their minimum distance of 5.46 x 1010 meters?
Q10: What is the force of gravity between Earth (5.972 × 1024 kg) and Mars (6.39 × 1023 kg) when they are at their maximum distance of 4.01 x 1011 m?
Q11: What is the distance between Earth (5.972 × 1024 kg) and Mars (6.39 × 1023kg) when the force of gravity is 5.1 x 1015?
Q12: What is the mass of a planet that has a force of 1.94 x 1017 N when away 1.0 x 1011 m from 5.972 x 1024 kg Earth?
Universal Gravitation Practice Quiz
Links
- On to the Circular Motion Page
- Back to the main Universal Gravitation and Circular Motion Page
- Back to the Stickman Physics Home Page
- Equation Sheet