Angular Launch Problems - StickMan Physics

Angular Launch Projectile Motion Problems

Break the angular launch into vertical and horizontal velocity components and learn to solve these projectile motion problems.

Learning Targets

I can break an angular launch into vertical and horizontal velocity components
I can use my knowledge of projectiles to pick givens and solve problems

Watch the lesson or read through and practice with the content below.

When an object is launched at an angle, it will have a velocity that can be broken into an X-axis component (v_x) and an initial Y-axis component (v_iy).

The X-axis velocity component (v_x) is constant and will not accelerated so it will stay the same the entire flight
The initial Y-axis velocity component will change as it accelerated by gravity 10 m/s² down. This is why we say (v_iy) and not just v_ybecause it will change throughout the problem.

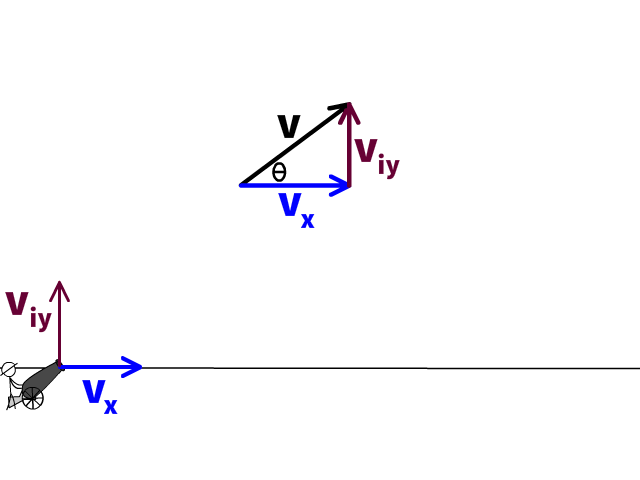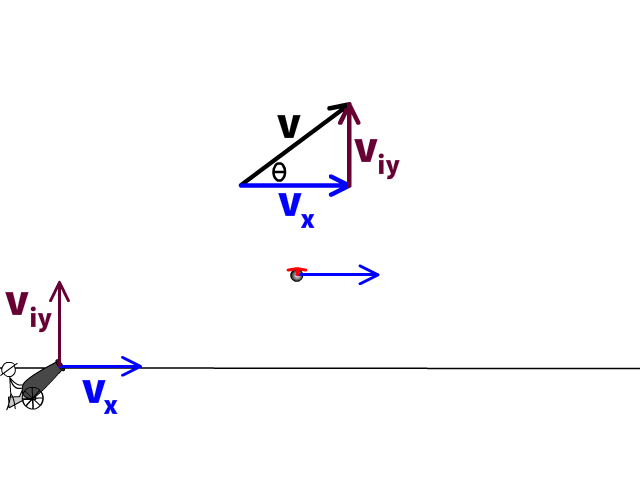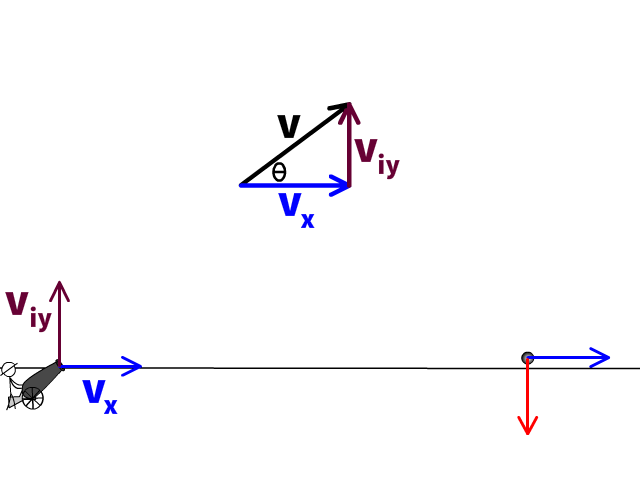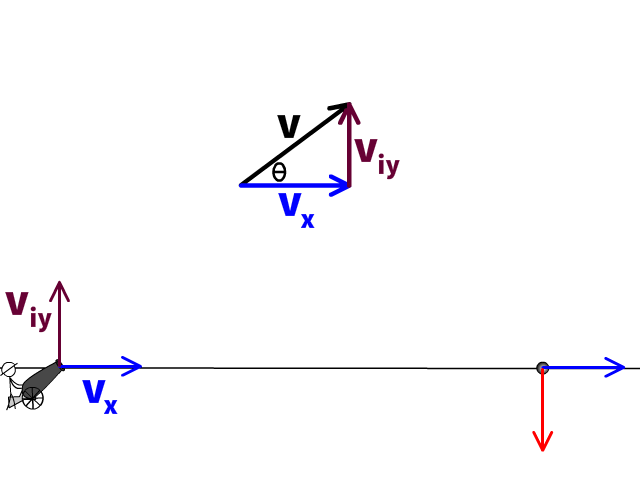
Horizontal Velocity

Horizontal velocity (v_x) will remain the same during a projectile's flight. We are assuming ideal conditions with no air resistance on all our examples on this page.

Vertical Velocity Assumptions

Depending on what the problem asks, we may be able to make assumptions about final velocity (v_fy)

Highest Point

If the problem asks us to find the highest point, the final velocity (v_fy) is 0 m/s.

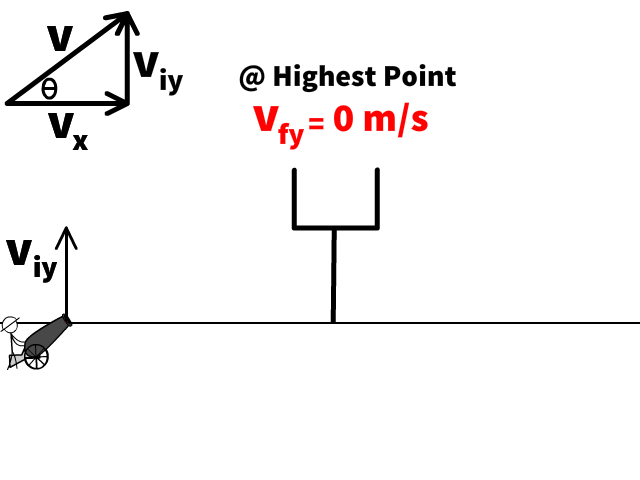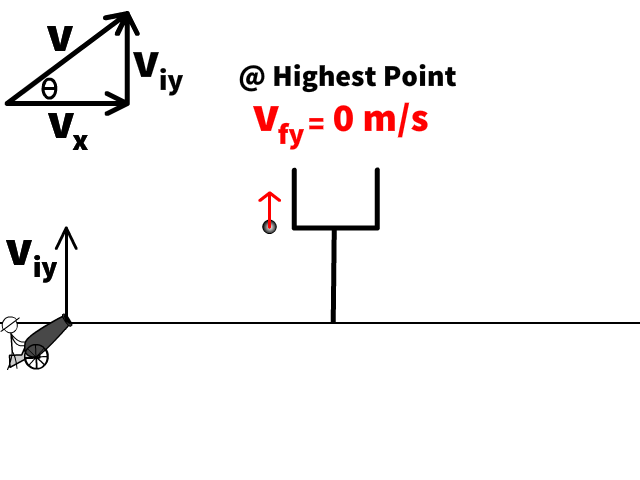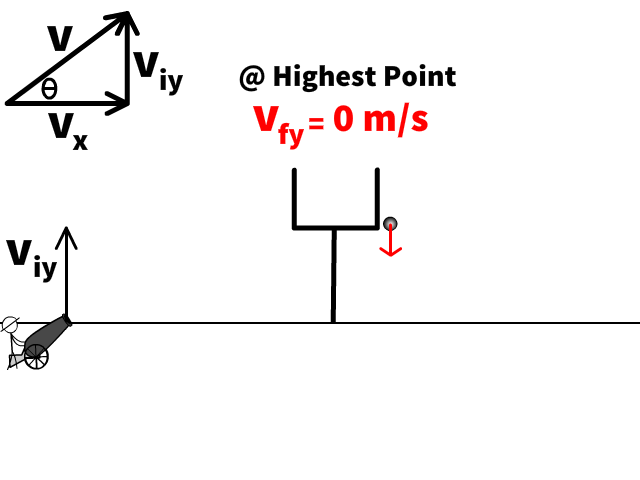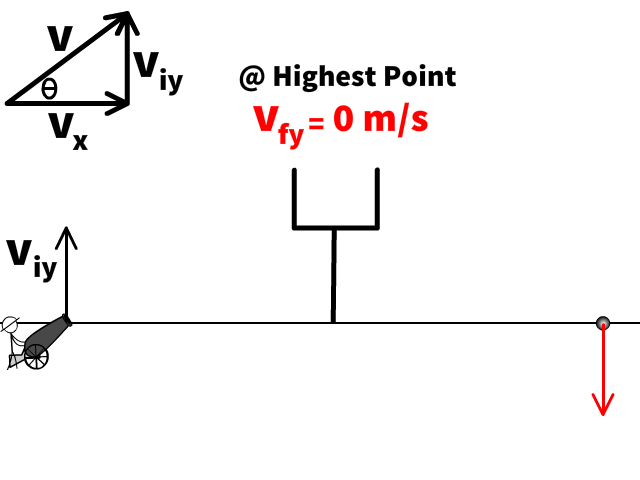
Furthest Point Landing at the Same Level

If the problem asks us to find the furthest point while landing at the same level, the final velocity (v_fy) is equal to the magnitude of the initial Y velocity component (v_iy) but in the reverse direction. (v_fy= -v_iy)

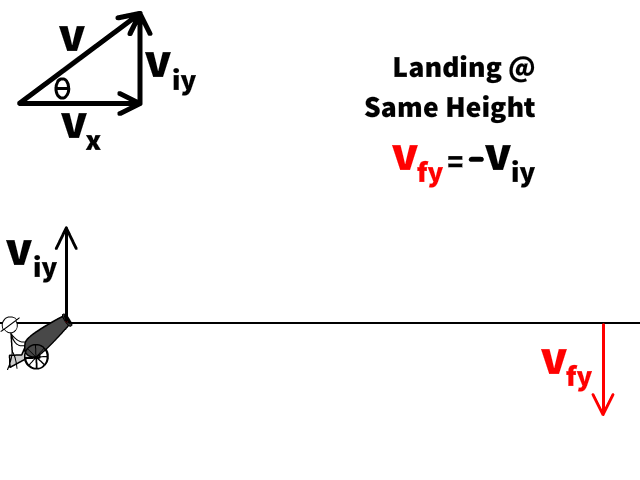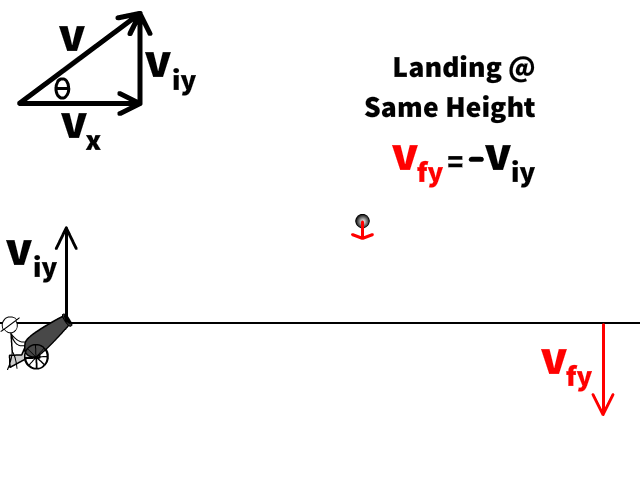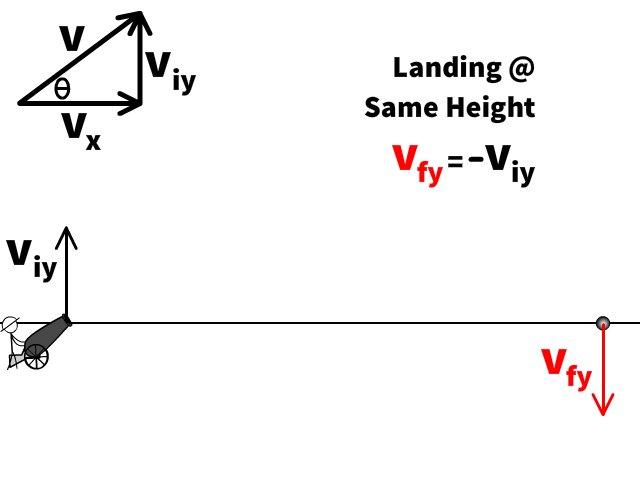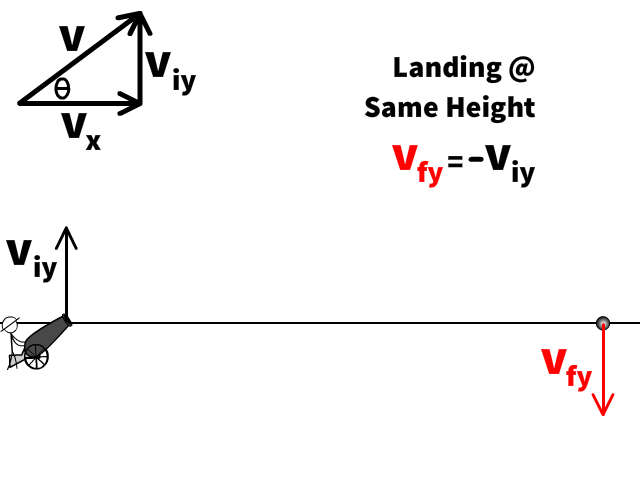
You must read into the problem to determine if you can make the v_fyassumptions. You can't make assumptions if the problem asks after so many seconds or after so much distance. One of our later problems will be an example.

Equations of Projectile Motion

Look below to see the 1D motion equations. They can be specialized to projectile motion.

X-Axis Specialization

The X-axis velocity is constant with (v) replaced by (v_x)

Y-Axis Specialization

(a) is substituted with a constant (g)
- In physics a constant, just means the number will be the same anywhere in a location. On Earth, g = 10 m/s² down
For displacement, (y) replaces (x)vrepresenting the Y-axis
Initial velocity (v_i) is replaced with (v_iy) to represent initial velocity in the Y-axis
Final velocity (v_f) is replaced with (v_fy) to represent final velocity in the Y-axis
These are the still same equations as the 1D motion equations.

Calculator Check: Make sure the mode of your calculator is in degrees for the examples

Breaking velocity at an angle into v_{x and}v_fy

(Q1-Q4) A cannon ball is shot at 60 m/s at an angle of 20° above the horizontal

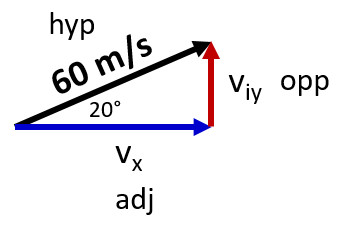
Q1: What is its initial X component of velocity (v_x)?

Adj = (cos Ө)(hyp)

Adj = (cos 20)(60)

Adj = 56.4 m/s Forward

Q2: What is its initial Y component of velocity (v_iy)?

Opp = (sin Ө)(hyp)

Opp = (sin20)(60)

Opp = 20.5 m/s Upwards

A cannon ball is shot at 60 m/s at an angle of 20° above the horizontal

Continuing with the givens solved for in Q1 and Q2 we now know the following information we can start populating a separate X and Y givens list as seen here to answer the following questions.

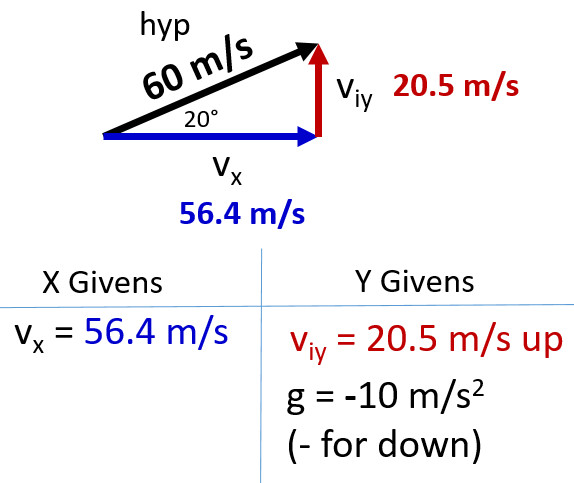
Examples Where You Can Infer v_fy

A cannon ball is shot at 60 m/s at an angle of 20° above the horizontal

Q3: What is the highest the cannonball gets?

At the highest point v_fy = 0 m/s. We don't need any X-axis information to answer this question.

Q4: How far downrange does the cannonball land at the same height?

Here the ball lands at the same height so you can assume v_fy

Add the given v_fy = -v_iy
Next you can solve for the time to land using the Y-axis givens and the best acceleration equation
Then solve for x using the X-axis givens and the constant motion equation

X = 231.2 m

(Q5-Q9) A soccer ball is kicked at 30 m/s at an angle of 25° above the horizontal.

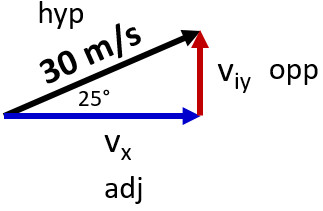
Q5: What is its initial X component of velocity (v_x)?

Adj = (cos Ө)(hyp)

Adj = (cos 25)(30)

Adj = 27.2 m/s Forward

Q6: What is its initial Y component of velocity (v_iy)?

Opp = (sin Ө)(hyp)

Opp = (sin25)(30)

Opp = 12.7 m/s Upwards

A soccer ball is kicked at 30 m/s at an angle of 25° above the horizontal.

Continuing with the givens solved for in Q5 and Q6 we now know the following information we can start populating a separate X and Y givens list as seen here to answer the following questions.

Q7: What is the maximum height the soccer ball reaches?

At the highest point v_fy = 0 m/s. We don't need any X-axis information to answer this question.

Q8: How far out does the soccer ball land?

Example Where You Can't Infer v_fy

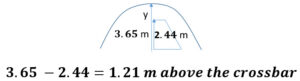
Q9: A soccer ball is kicked at 30 m/s at an angle of 25° above the horizontal. If a soccer goal crossbar is 2.44 meters above the ground. How much over or under the crossbar is the ball 9 meters downrange?

This is a continuation and we already solved for the starting givens here. We can't assume 9 meters downrange is at the top of flight or landing spot. Click see answer when you are ready to see the steps to the solution.

You know that the question asks about 9 meters downrange which is our X. You can't assume this is at the highest height or when it lands.

Part 1: Use the new X information to solve for t using the X-axis.

Next for Part 2 you can populate the Y-axis givens with the t = 0.33 s just solved for.

Now we can choose an acceleration equation and solve for y

Part 3: Now you know how high the soccer ball after 9 meters down range and you can answer the question. How much higher the y of 3.65 m taller than the crossbar of 2.44 meters.