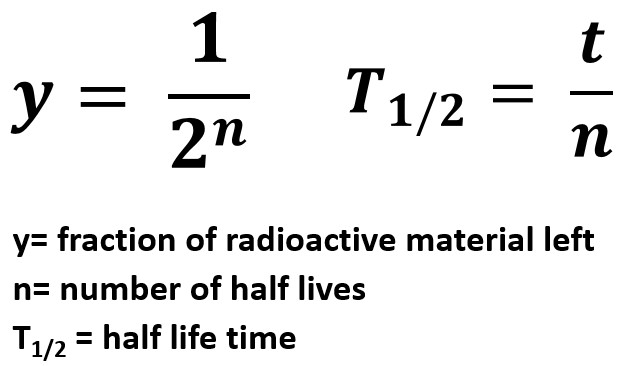Half-Life

Half-Life

Radioactive elements goes through decay at different rates. The time it takes for the element to degrade by half is called a half-life. Learn more here.

Half-Life Learning Targets:

  • I understand the meaning of a radioactive isotope half-life
  • I can determine the amount of radioactive substance remaining after an amount of time (mathematically and visually with a table)
  • I can determine the amount of radioactive substance remaining after a number of half lives (mathematically and visually with a table)

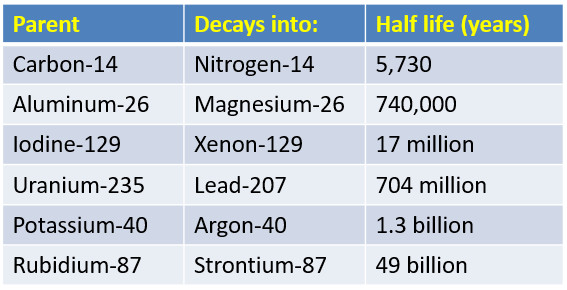
Half Life of Common Radioactive Isotopes

A half-life is the time it takes for half of the radioactive sample to decay.

  • Half lives range from a fraction of a second to billions of years.
  • The length of a half life is shorter the less stable the radioactive isotope.

Radiometric Dating

Radiometric dating is a process of determining the age of an object by the amount of radioactive isotope that has degraded from an initial sample.

Carbon-14 is a radioactive form of carbon used for radiometric dating of once living organisms.

Carbon-14 has a half-life of 5,730 years.  All life molecules have Carbon, testing the amount of radioactive carbon present in a sample can determine its age.

An archaeologist that tests a bone and finds it has half the normal amount of radioactive carbon-14 just determined its age is 5,730 years old.

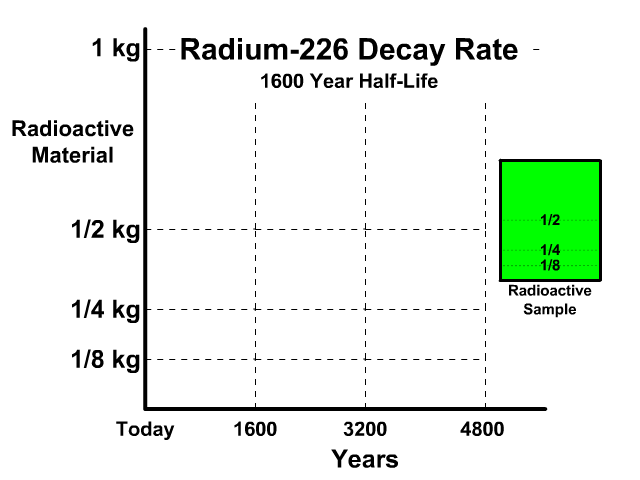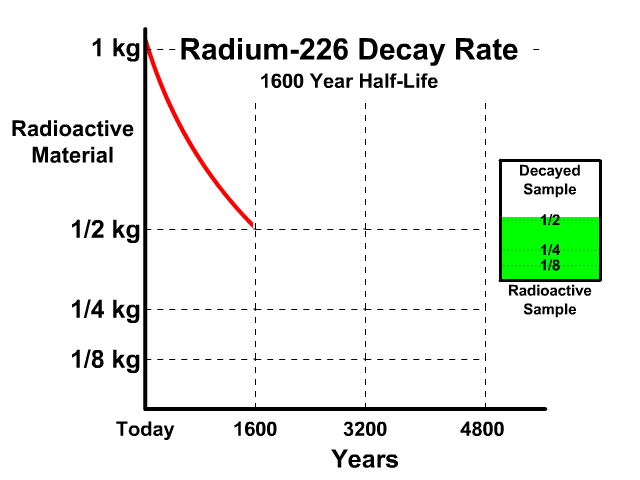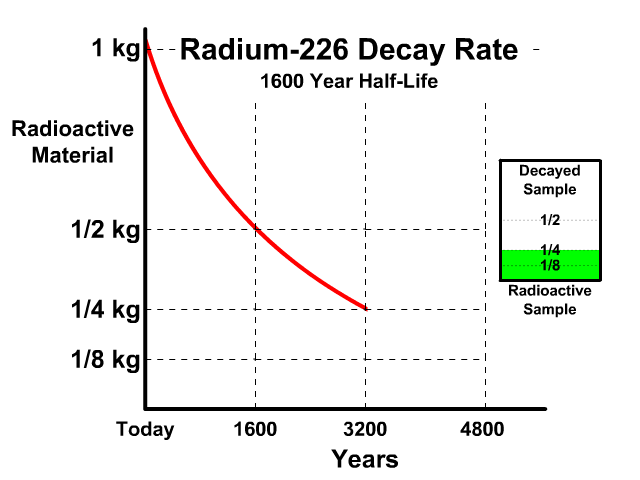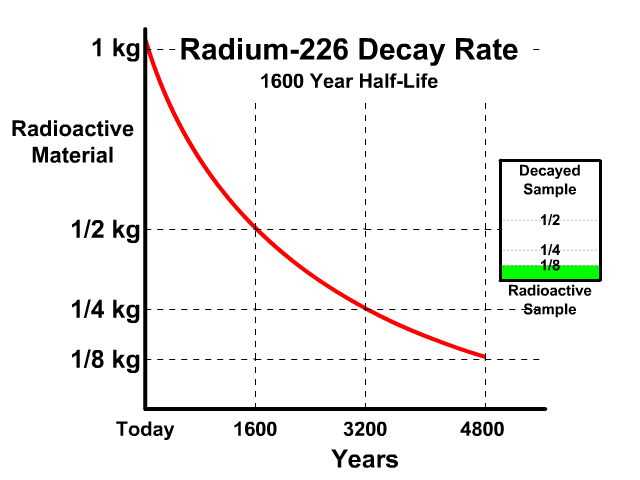
The half-life of Radium-226 is 1600 years.  This means a 1 kg radioactive sample today would decay to a 1/2 kg radioactive sample after 1600 years.

Analyze the table along with the animation to identify the pattern and relationship between number of half-lives, kilograms of radioactive sample size, nonradioactive sample size, and percent decayed.

 Half Lives Radioactive Nonradioactive Percent Decayed
0 1 kg 0 kg 0%
1 1/2 kg 1/2 kg 50%
2 1/4 kg 3/4 kg 75%
3 1/8 kg 7/8 kg 87.5%

Half Life Equations

We will work through a few sample problems on this page using a table form and the following equations.

y=1/(2n)

T1/2 = t/n

  • y represents the fraction of radioactive material remaining
  • n represents the number of half lives
  • T1/2 represents the length of one half life

Guided Half-Life Example

A. How much of the original radioactive material remains after four half-lives?

Givens List:

    • n = 4
    • y=?

Equation:

    • y=1/(2n)

Work:

    • y=1/(24)
    • y= 1/16 or 0.0625

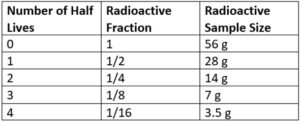
B. How much of a 56 gram radioactive sample radioactive remains after four half-lives?

First: Find the fraction left

Givens List:

    • n = 4
    • y=?

Equation:

    • y=1/(2n)

Work:

    • y=1/(24)
    • y=0.0625

Second: Multiply the fraction by the original sample size

0.0625 x 56 grams = 3.5 grams of a radioactive sample remains

Using a table to answer example A and B above

#1 Make a table as seen below starting with 0 half lives and columns for any necessary information.  Fill in one in this column if asked about a fraction, fill in 100% if asked about a percent.

#2 Fill in the table with an extra row for every half life until you get to the number of half-lives in the question

Radioactive Half-Life Table

#3 The completed table here could be used to answer questions about the fraction or sample remaining for up to four half-lives of a 56 gram sample.

Completed Half-Life Table

C. How long is a half-life for a substance that has 2.5 half lives every 50,000 years?

Givens:

    • n = 2.5
    • t = 50,000 years
    • T1/2 = ?

Equation:

    • T1/2 = t/n

Work:

    • T1/2 = 50000/2.5
    • T1/2 = 20,000 years

D. A 100 gram unknown radioactive material has a half-life of 4000 years. How many grams of the radioactive sample will remain after 20,000 years?

Step 1: Determine the number of half-lives

Givens: 

    • T1/2 = 4000 years
    • t = 20,000 years

Starting Equation:

    • T1/2 = t/n   rearranges to n = t/T1/2

Work:

    • n = 20000/4000
    • n = 5

Step 2: find the fraction left after five half-lives

Givens: 

    • y = ?
    • n = 5

Equation:

    • y =1/(2n)

Work:

    • y =1/(25)
    • y = 0.03125

Step 3: Multiply the fraction by the original sample mass

0.03125 x 100 g = 3.125 grams

Example Problems

Note: You can use a table or math for any of the following examples

1. What percentage of radioactive substance remains after ten half-lives?

y = 1/(2n)

y = 1/(210)

y = 0.0009765625

Multiply by 100 to get a percent from a fraction

0.0009765625 x 100 = 0.098 percent

2. If a substance starts out with 400g, how much remains after five half-lives?

Make a table and cut 400 grams in half five times

Number of Half Lives Radioactive

Sample Size
0 400 kg
1 200 kg
2 100 kg
3 50 kg
4 25 kg
5 12.5 kg

12.5 kg of radioactive substance remains

3. How many complete half-lives have occurred if 12.5% of the original radioactive material remains?

Start with 100% and keep on adding a half life until you get to 12.5%

Number of Half Lives Radioactive percent
0 100%
1 50%
2 25%
3 12.5%

3 half-lives occurred

4. How many complete half-lives have occurred is 18.75 grams of an originally 600 gram radioactive substance remains?

Make a table and cut the 600g sample in half until you get to 18.75 grams

Number of Half Lives Radioactive Sample
0 600g
1 300g
2 150g
3 75g
4 37.5g
5 18.75g

After 5 half lives a 600 g sample decays to 18.75 grams

Links

Terms and Conditions - Privacy Policy