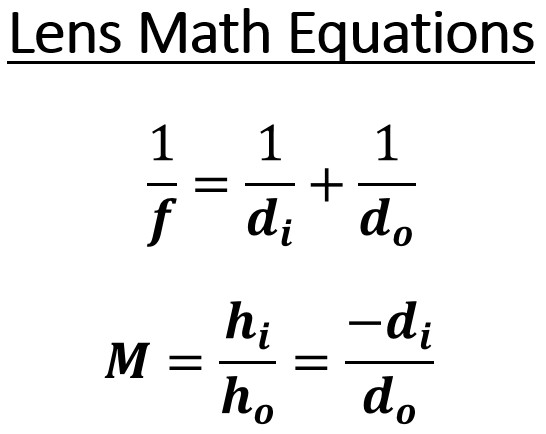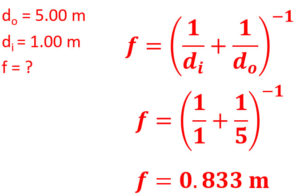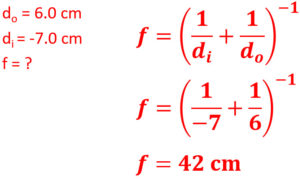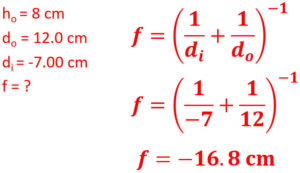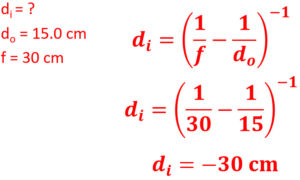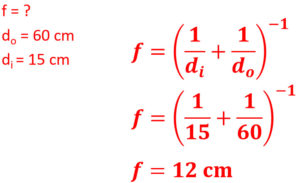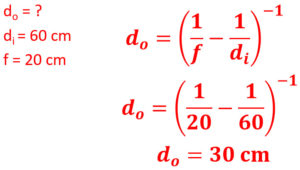Lens Math
Learn how to use equations with lens math to determine information about the image like height and distance from the lens.
Lens Math Variables
| Name | Variable | Unit | Unit Abbreviation |
| focal length | f | centimeters or meters | cm or m |
| distance to image | di | centimeters or meters | cm or m |
| distance to object | do | centimeters or meters | cm or m |
| magnification | M | times | x |
| height of image | hi | centimeters or meters | cm or m |
| height of object | ho | centimeters or meters | cm or m |
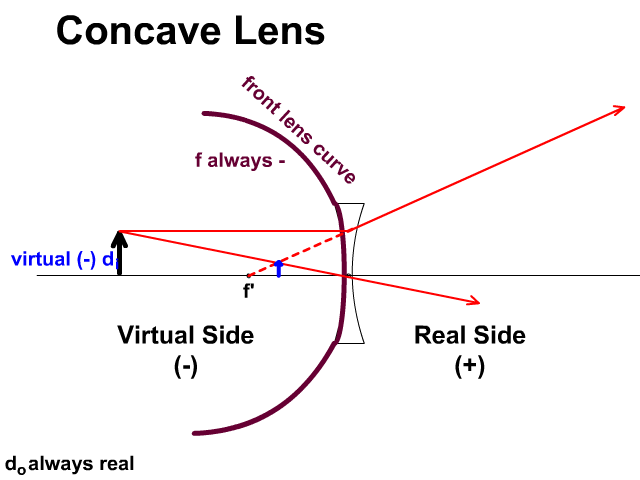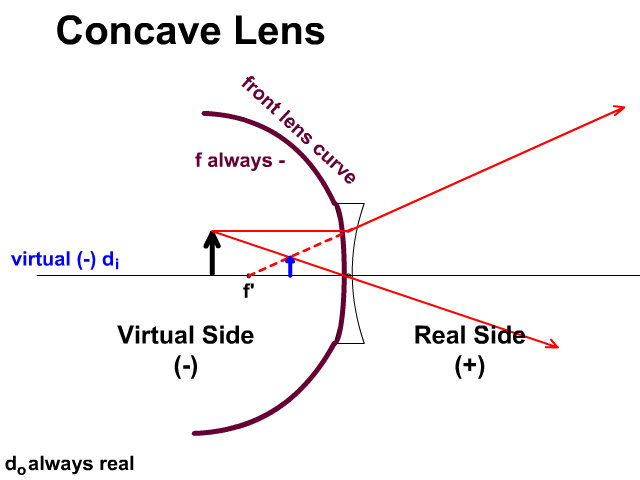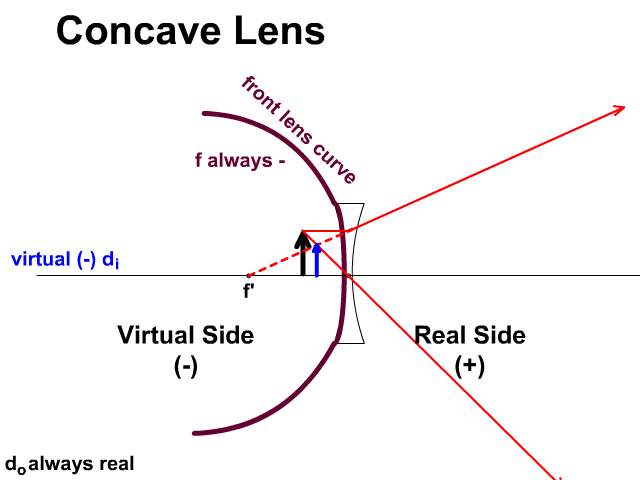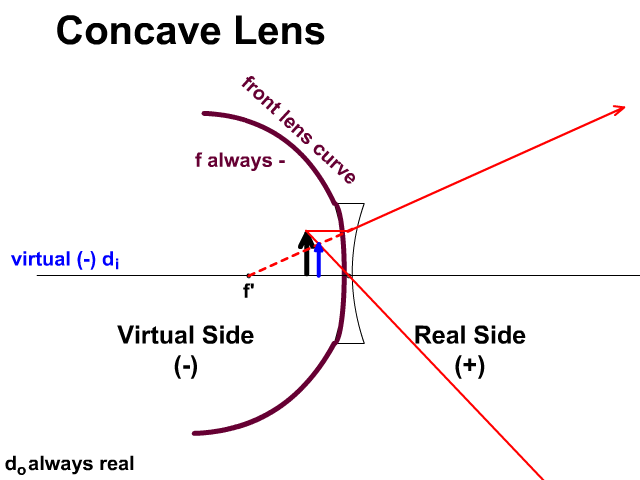
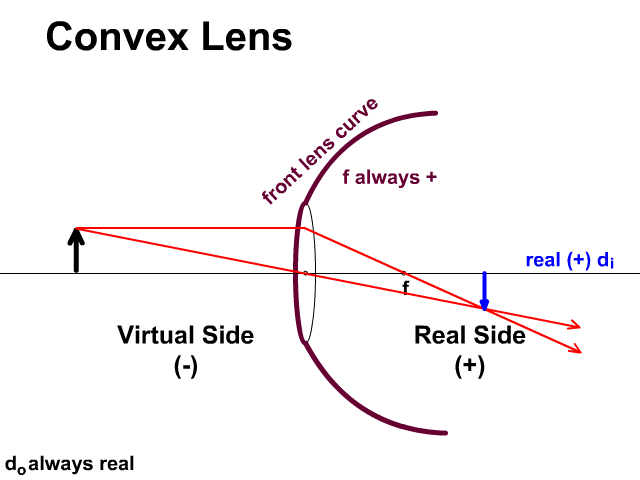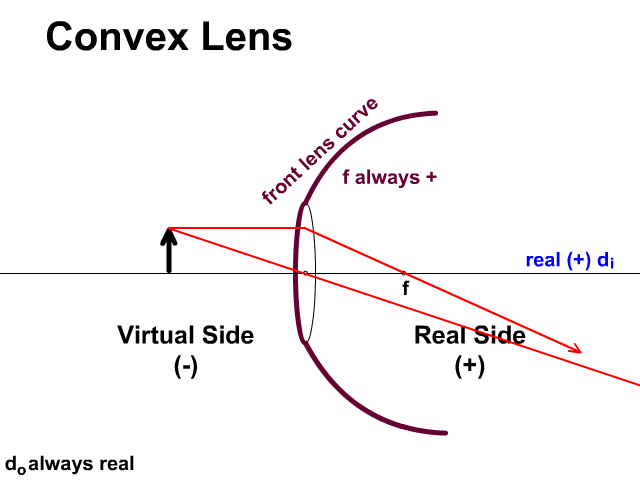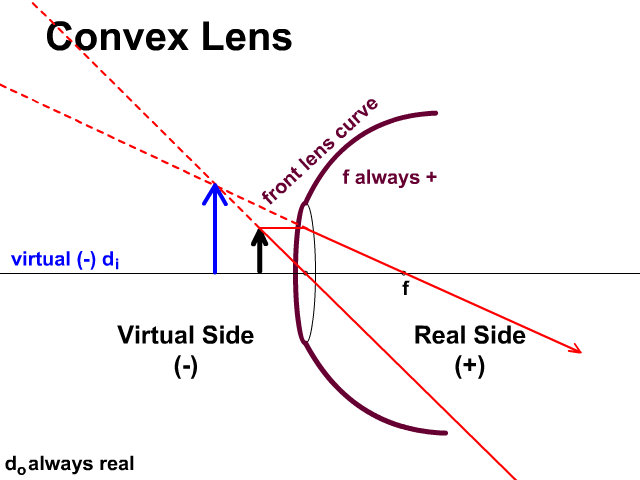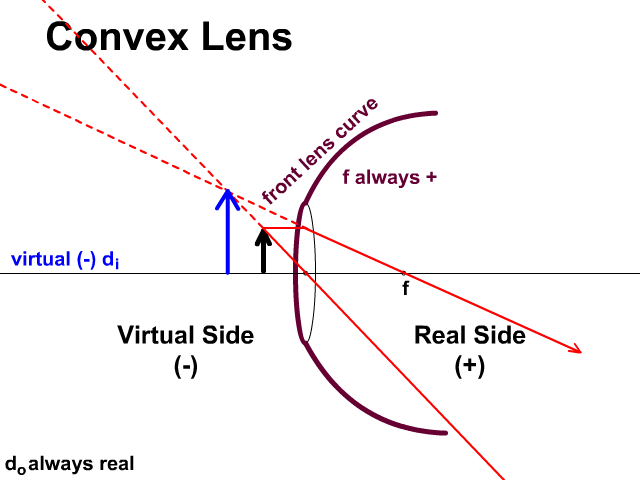
Virtual and Real Sides of a Lens
Light travels through a lens unlike a mirror which reflects. Light travels to the real side given a positive (+) which is on the opposite side of the object. If the image appears on the real side it will be given a positive value. If the image appears on the virtual side, side of the object, it is virtual and given a negative symbol.
Lens Math Facts
- For all lenses:
- do is always positive + no matter what, an object is always real
- For a concave lens:
- (only produce, virtual, upright, reduced images)
- f is always negative (-)
- concave lens focal distances will be negative during math since the curve of the front side is toward the virtual side.
- di is always negative (-)
- because concave lenses only produce virtual upright images
- For a convex lens:
- f is always positive (+)
- convex lens focal distances will be positive since the curve of the front side is toward the real side.
- di can be positive or negative. You will determine this by the solution for di.
- If di is a positive in your solution, the image is real and inverted.
- If di is a negative in your solution, the image is virtual and upright.
Lens Equation Tips
do
- First of all the object is always real and do will always be positive, never make this negative and if a solution is negative, you did something wrong.
di
- If a problem says you have a virtual image, make the di negative. If a problem says that the image appears on the same side as the object, make the di negative.
- A real image is always inverted, a virtual image is always upright.
f
- If you have a concave lens the f will always be negative
- If you have a convex lens the f will always be positive
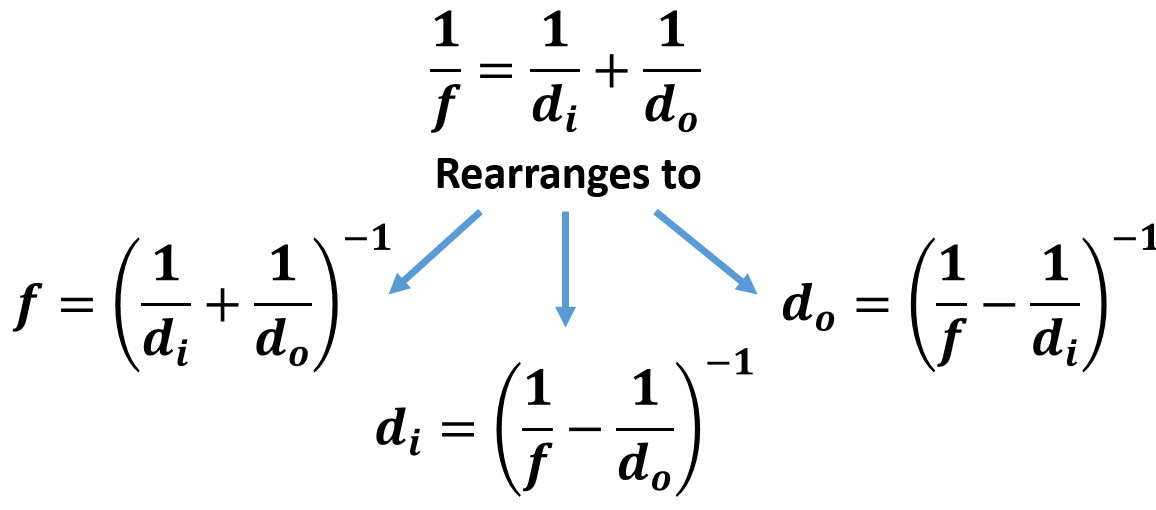
This equation can be used three ways
- (hi / ho ) = (di / -do )
- M= hi / ho
- M= -di / do
M
- you can solve for M with hi and ho
- M= hi / ho
- you can solve for M with di and do
- M= -di / do
- If M is 1 the image is not magnified
- If M is less than 1 the image is reduced
- If M is greater than 1 the image is enlarged
- If M is negative the image is real and inverted
- If M is positive the image is virtual and upright
Example Problems
Use the video provided for extra support through these questions.
1. An object is 5.00 meters away from a convex lens, which produces a real image 1.00 meters away. What is the focal length of the lens?
2. An object is 5.00 meters away from a convex lens, which produces a real image 1.00 meters away. What is the magnification of the image?
3. An object is 6.0 centimeters away from a convex lens, which produces a virtual image 7.0 centimeters away. What is the focal length of the lens?
4. A 2 cm tall object is 6.0 centimeters away from a convex lens, which produces a virtual image 7.0 centimeters away. What is the height of the image?
5. An 8 cm tall object is 12.0 centimeters away from a concave lens, which produces a virtual image 7.0 centimeters away. What is the focal length of the lens?
6. An 8 cm tall object is 12.0 centimeters away from a concave lens, which produces a virtual image 7.0 centimeters away. What is the height of the image?
7. Find the image distance for a convex lens with an object distance of 15 cm and a focal length of 30 cm.
8. Given di = -18 cm, do= 6 cm, and M=3, describe the image.
9. Find the focal length for a convex lens with an object distance of 60 cm and an real image distance of 15 cm.
10. Find the distance an object is away from a convex lens with an real image formed 60 cm away and a focal length of 20 cm.
PhET Lens Lab
Return to the previous section by clicking here to complete a PhET lens lab that includes lens math.
Links
- Back to the Main Electromagnetic Waves Page
- Back to the Stickman Physics Home Page
- Equation Sheet