The relationship between density and pressure explains how fluid density directly affects gauge pressure at a given depth. Governed by the equation Pgauge = ρgh, this principle highlights how denser fluids create higher pressures. Understanding this relationship is key to analyzing fluid behavior and its practical applications in physics and engineering.
Atmospheric Pressure in a fluid at a given depth is determined using the equation:
P = P₀ + ρgh
This includes both atmospheric pressure (P₀) and the pressure from the fluid column (ρgh). However, we can simplify this to gauge pressure, Pgauge = ρgh, by focusing only on the pressure contribution from the fluid itself. This simplification is useful in most practical applications where relative pressure differences are more important than absolute pressure.
Where:
- P: Absolute pressure at depth (Pa)
- P₀: Atmospheric pressure at the surface (101,325 Pa)
- ρ: Density of the fluid (kg/m³)
- g: Gravitational field strength (9.8 N/kg on Earth)
- h: Depth of the fluid (m)
Key Insight
From the equation Pgauge = ρgh, we can observe that the pressure due to the fluid column is directly proportional to the fluid’s density (ρ). This means if the density of the fluid doubles, the pressure due to the fluid column at the same depth will also double.
Derivation to Show Ratio Relationships
To calculate how pressure changes with fluid density, start with the simplified gauge pressure formula:
Pfluid = ρgh
Now, let’s compare the pressure for two scenarios:
Scenario 1: Initial Density (ρ1):
P1 = ρ1gh
Scenario 2: Doubled Density (ρ2 = 2ρ1):
P2 = ρ2gh = (2ρ1)gh = 2(ρ1gh)
Ratio of Pressure (P2to P1):
P2/P1 = 2(ρ1gh)/(ρ1gh) = 2
Conclusion
When the fluid’s density doubles, the pressure at the same depth also doubles. This direct proportionality simplifies predicting how changes in density affect pressure.
Practical Examples
- Oil vs. Water
Oil typically has a lower density than water (e.g., 850 kg/m3 vs 1,000 kg/m3). At the same depth, the pressure in oil is lower than in water. - Mercury vs. Water
Mercury, with its very high density (13,600 kg/m3), exerts significantly higher pressure than water. For example, at 1 meter:- Pressure due to water:
- Pwater = (1,000)(9.8)(1) = 9,800 Pa
- Pressure due to mercury:
- Pmercury = (13,600)(9.8)(1) = 133,280 Pa
- Pressure due to water:
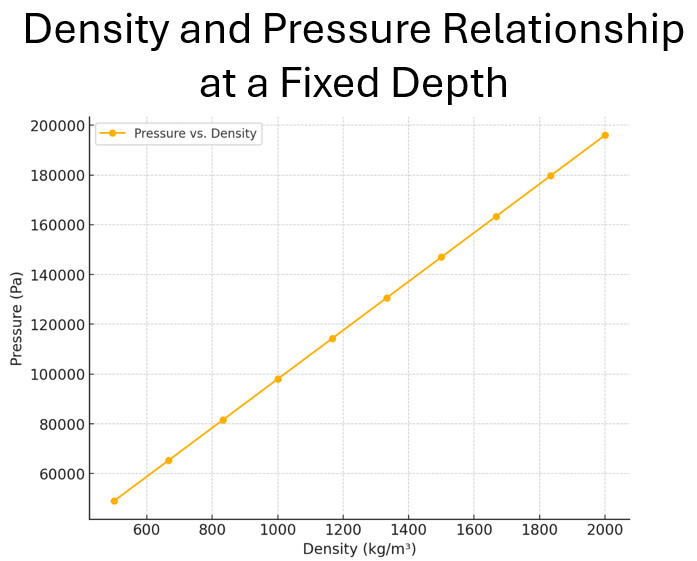
Graphical Representation of Gauge Pressure and Density at a Given Depth
A graph can illustrate the direct proportionality between density and gauge pressure. On the graph:
- X-axis: Fluid density (ρ)
- Y-axis: Gauge pressure (Pgauge)
The data is governed by the equation:
Pfluid = ρgh
Where:
- Pfluid: Gauge Pressure (Pa)
- ρ: Fluid density (kg/m³)
- g: Gravitational field strength (9.8 N/kg on Earth)
- h: Depth (10 m)
At a fixed depth of (10 m), the relationship remains linear, showing that as density increases, pressure increases proportionally.

| Density and Pressure Data at h=10m | ||
| Density (kg/m3) | Pressure (Pa) | |
| 1 | 500.0 | 49000.0 |
| 2 | 667.0 | 65300.0 |
| 3 | 833.0 | 81700.0 |
| 4 | 1000.0 | 98000.0 |
| 5 | 1167.0 | 114300.0 |
| 6 | 1333.0 | 130700.0 |
| 7 | 1500.0 | 147000.0 |
| 8 | 1667.0 | 163300.0 |
| 9 | 1833.0 | 179700.0 |
| 10 | 2000.0 | 196000.0 |
Conclusion
Pressure in a fluid increases proportionally with density, as shown by Pgauge = ρgh. This explains why denser fluids exert greater pressure and is key to understanding real-world applications like hydraulic systems and barometers.
Links: