Pressure in Fluids: Exploring P = F/A and Depth Factors

Pressure in fluids is a fundamental concept in fluid statics and dynamics, and it helps explain how forces are distributed in liquids and gases. This lesson dives into the physics of pressure, covering its mathematical representation, real-world applications, and how depth and fluid density impact it.

---

What is Pressure?

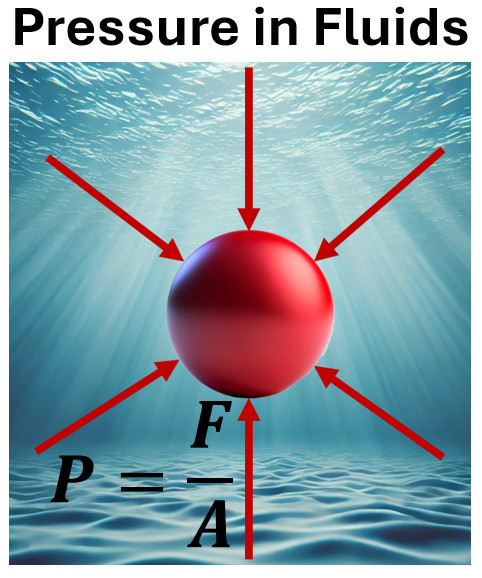
Pressure is the force exerted per unit area on the surface of an object. Mathematically, it’s represented as:
P = F/A
Where:

• P: Pressure (in Pascals, Pa)
• F: Force (in Newtons, N)
• A: Area (in square meters, m²)

For example, the pressure exerted on the ground by a person standing on one foot is higher than when standing on both feet, as the force is spread over a smaller area in the first case.

---

Factors That Affect Pressure in Fluids

1. Depth and Pressure Relationship
   The deeper you go into a fluid, the greater the pressure. This relationship is captured by the equation:
   P = P₀ + ρgh
   Where:

• P: Absolute pressure at a given depth
• P₀: Atmospheric pressure at the surface (around 101,325 Pa or 14.7 psi at sea level)
• ρ: Fluid density (kg/m³)
• g: Gravitational field strength (9.8 N/kg on Earth which is equivalent to 9.8 m/s²)
• h: Depth of the fluid (m)

Key Insight:

• As depth (h) increases, pressure increases linearly. This explains why scuba divers need special suits to withstand the high pressure in deep water.

2. Fluid Density
   Denser fluids exert more pressure at the same depth. For instance, mercury, with its high density (13,600 kg/m³), generates much higher pressure than water (1,000 kg/m³) at an equivalent depth. Learn more about density vs. pressure at a fixed depth here
3. Gravitational Field Strength
   In stronger gravitational fields, like on Jupiter, the pressure at the same depth would be much higher compared to Earth.

---

Applications of Pressure in Fluids

• Gauge Pressure vs. Absolute Pressure
  • Gauge Pressure (P_gauge = ρgh): Pressure measured relative to atmospheric pressure.
  • Absolute Pressure (P = P₀ + ρgh): Total pressure, including atmospheric pressure.

For example, a tire’s gauge pressure only reflects the pressure inside the tire relative to the atmosphere, but the actual pressure acting at the valve is absolute pressure.

---

Atmospheric Pressure and Its Role in Fluid Mechanics

Atmospheric pressure, often abbreviated as ATM, is the pressure exerted by the weight of the Earth’s atmosphere on everything at the surface. At sea level, the atmospheric pressure is approximately:

• 14.7 psi (pounds per square inch)
• 101,325 Pascals (Pa)
• 1 Atmosphere (ATM)

This baseline pressure is critical for a variety of natural and technological processes, making it a foundational concept in fluid mechanics.

---

Importance of Atmospheric Pressure

1. Breathing and Human Physiology
   The atmospheric pressure around us ensures that oxygen is delivered efficiently to our lungs. Without sufficient atmospheric pressure, oxygen would not diffuse properly into our bloodstream. At higher altitudes, where atmospheric pressure decreases, this reduced oxygen availability is why people may experience altitude sickness.
2. Aviation
   Airplanes must be pressurized because atmospheric pressure decreases as altitude increases. For instance, at 35,000 feet, the atmospheric pressure is only about 0.2 ATM. Without pressurization, humans wouldn’t be able to breathe or function properly at such altitudes.
3. Pressure Comparisons in Fluids
   Atmospheric pressure forms the baseline for measuring absolute pressure (P) in fluids. For example:
   P = P₀ + ρgh
   Here, P₀ represents atmospheric pressure, which adds to the gauge pressure caused by the weight of a fluid column.

---

Understanding 1 ATM

At sea level, 1 ATM is equivalent to the pressure exerted by a column of mercury 760 mm high in a barometer. This value is so standardized that it’s often used in experiments, calculations, and real-world applications.

• Conversions:
  • 1 ATM = 101,325 Pa
  • 1 ATM = 760 mmHg
  • 1 ATM ≈ 14.7 psi

---

Practical Examples and Applications

1. Boiling Point Variation
   Atmospheric pressure affects the boiling point of liquids. At higher altitudes, where pressure is lower, water boils at temperatures below 100°C. This is why cooking instructions often vary for high-altitude locations.
2. Fluid Pressure Measurements
   Atmospheric pressure is a reference point for gauge pressure and absolute pressure. For instance, a car tire may read 32 psi on a gauge, but its absolute pressure is 32 psi + 14.7 psi (atmospheric pressure).

---

Additional Resources

For more details about atmospheric pressure and its significance, check out the following resources:

• NASA Atmospheric Pressure Overview
• Physics Hypertextbook: Pressure
• Science Direct: Atmospheric Pressure and Its Effects

---

Why is Pressure a Scalar Quantity?

Pressure is considered a scalar quantity because it has magnitude but no specific direction. Unlike vector quantities, which include both magnitude and direction (such as force or velocity), pressure applies equally in all directions at a given point within a fluid.

Equal Distribution in Fluids:
Fluids, such as liquids and gases, consist of particles that move freely in every direction. When you apply force to a fluid, it distributes evenly throughout. As a result, pressure acts uniformly in all directions, without favoring a particular orientation.

Mathematical Explanation:
To better understand, let’s examine the formula for pressure: P = F/A (force divided by area). The force’s directional components cancel each other out within the fluid. What remains is only the scalar magnitude of the pressure, which does not depend on direction.

Practical Examples

1. When you are underwater, pressure surrounds your body equally, no matter how you are positioned.
2. Similarly, air in a sealed container exerts pressure uniformly in all directions. This ensures there is no directional bias within the container.

---

Interesting Facts About Pressure

1. Pressure in Everyday Life
   • Walking on snow with snowshoes exerts less pressure, preventing sinking.
   • Hydraulic systems, like car brakes, use fluid pressure to transmit force efficiently.
2. Pressure Underwater
   At 10 meters of depth in water, the pressure increases by approximately 1 atmosphere (101,325 Pa) due to the weight of the water column above.

---

Pressure: Example Problems

1) A diver is 20 m underwater in the ocean. Calculate the absolute pressure they experience, assuming water density is 1,025 kg/m³. (Use atmospheric pressure of 101,325 Pa and a gravitational field strength of 9.8N/kg)

See Solution

---

Ratio Problems

2) If the density of a fluid doubles, how does the pressure at a given depth change?

See Solution

---

3) If you triple the depth in water, the pressure:
a) Stays the same
b) Doubles
c) Triples
d) Increases by a factor of 1.5

See Solution

Ranking Problem

4. Rank the following in terms of pressure at a depth of 5 m from greatest to least:

• Water (ρ = 1,000 kg/m³)
• Oil (ρ = 850 kg/m³)
• Mercury (ρ = 13,600 kg/m³)

See Solution

Learn more about density vs. pressure at a fixed depth here

---

Advanced Connections

1. Historical Context
   Evangelista Torricelli, the inventor of the barometer, first measured atmospheric pressure. His work laid the foundation for understanding fluid pressure.
2. Interdisciplinary Insight
   Understanding pressure has applications in biology (e.g., blood pressure), meteorology (e.g., predicting storms), and engineering (e.g., designing dams).

Links:

• Learn more about density vs. pressure at a fixed depth here
• Continue to Fluids and the Buoyant Force: F_b=ρVg
• Go back to the StickManPhysics AP Fluids Lessons Index
• See the StickManPhysics Table of Contents
• Go to our StickManPhysics Home Page