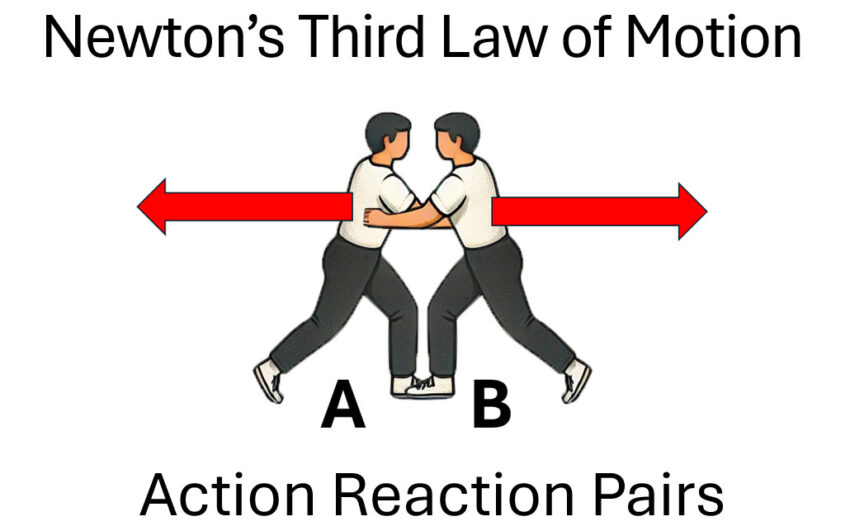
Newton’s Third Law of Motion states that forces come in equal and opposite action-reaction pairs. When object A applies a force on object B, object B simultaneously applies an equal and opposite force on object A. This principle is fundamental to understanding how forces interact in systems and is a cornerstone of physics.
Action-Reaction Forces in Motion
For example, as the wheels of a cart apply a backward force on the ground, the ground applies an equal and opposite force forward on the cart, propelling it. Newton’s Third Law also governs the force interactions between multiple objects, such as carts in a train system.
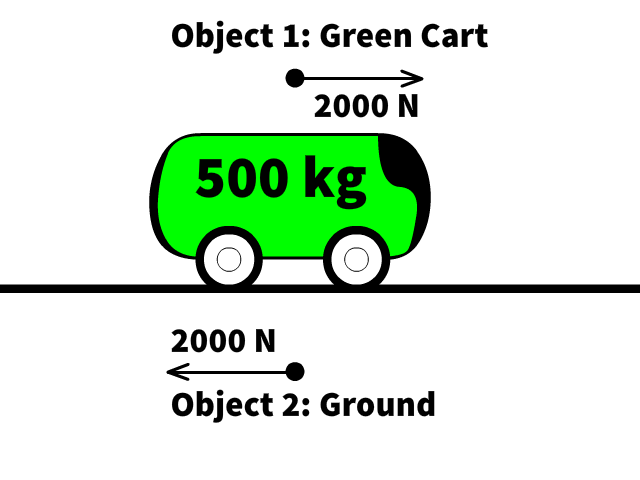
Force Interactions Between Carts
When a group of carts accelerates together at the same rate, the force interaction between them varies depending on the mass each cart must pull. While the forces between individual carts are equal and opposite, the magnitude of the force depends on the mass of the carts being pulled.
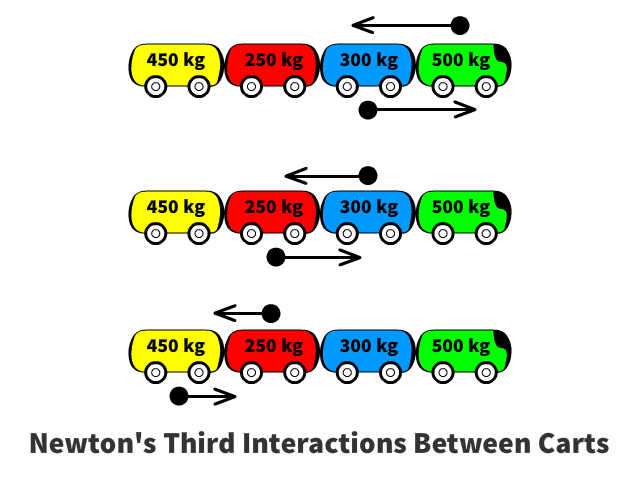
In the previous lesson we determined that the acceleration of the entire train from the 2000 N of force pulling the entire 1500 kg train to be 1.33 m/s2. Now lets determine the force interactions between each cart in order to get that system of carts mass to accelerate
Force Interaction Between the Blue Cart and the Green Locomotive
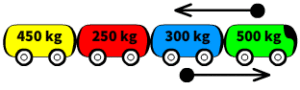
The combined mass of the blue, red, and yellow carts equals 1000 kg.
(300+250+450) = 1000 kg
Using Newton’s Second Law of Motion, Fnet = ma, we calculate the force needed to accelerate the system.
With an acceleration of 1.33 m/s2, the net force is Fnet = (1000)(1.33) = 1330 N.
According to Newton’s Third Law of Motion, the blue cart exerts an equal and opposite force of 1330 N on the green locomotive.
Force Interaction Between the Red and Blue Carts
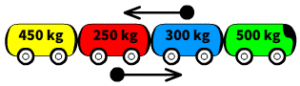
The combined mass of the red and yellow carts is 700 kg.
(250+450) = 700 kg
Using Newton’s Second Law of Motion, Fnet = ma, we calculate the net force required to accelerate the system.
With an acceleration of 1.33 m/s2, the net force is Fnet = (700)(1.33) = 931 N.
According to Newton’s Third Law of Motion, the red cart exerts an equal and opposite force of 931 N on the blue cart.
Force Interaction Between the Yellow and Red Carts
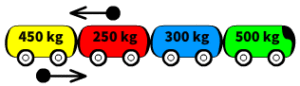
The yellow cart has a mass of 450 kg. Using Newton’s Second Law of Motion, Fnet = ma, we calculate the force needed to accelerate the yellow cart.
With an acceleration of 1.33 m/s2, the net force is Fnet = (450)(1.33) = 598.5 N.
By Newton’s Third Law of Motion, the yellow cart exerts an equal and opposite force of 598.5 N on the red cart.
Trends in Force Interaction Between Carts
Newton’s Third Law governs the force interactions between each cart in the system. Notably, the entire group of carts accelerates at the same rate, previously calculated to be 1.33 m/s2. However, the magnitude of the force interaction differs between carts. As you move further back in the system, each cart pulls less total mass, requiring less force to achieve the same acceleration. Despite this variation in force magnitude, Newton’s Third Law ensures that the forces between any two carts remain equal in size and opposite in direction.
Conclusion: Practical Applications of Newton’s Third Law
Newton’s Third Law of Motion plays a vital role in understanding and solving real-world problems across various fields. In transportation, it explains how propulsion systems, like those in cars and trains, generate motion. Engineers rely on this principle to design stable structures that balance forces effectively. In sports science, it helps explain how athletes generate and apply force to enhance their performance. By applying Newton’s Third Law, we can analyze complex systems of forces and predict how objects interact, offering valuable insights into motion in both theoretical and practical contexts.
Learn more about Newton’s Law Watching this PBS Crash Course on Newton’s Laws of Motion here.