Incline Planes: Forces on Angled Surfaces

Home » Unit 3: Newton’s Laws of Motion and Force » Incline Planes: Forces on Angled Surfaces

Incline Planes

Learn the forces involved in incline planes with and without friction. See how to solve for acceleration of an object created by the net force.

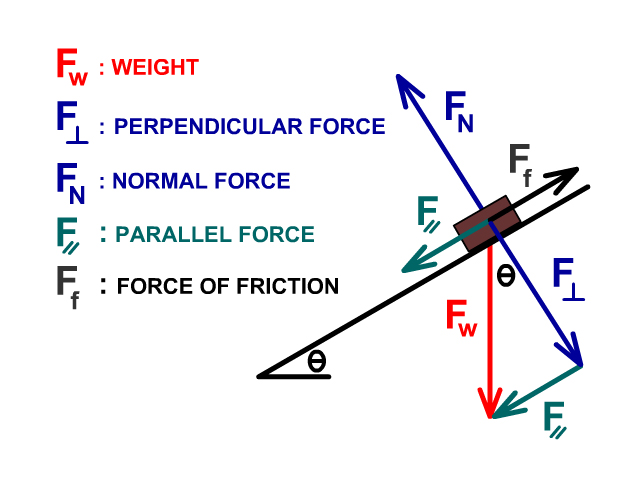
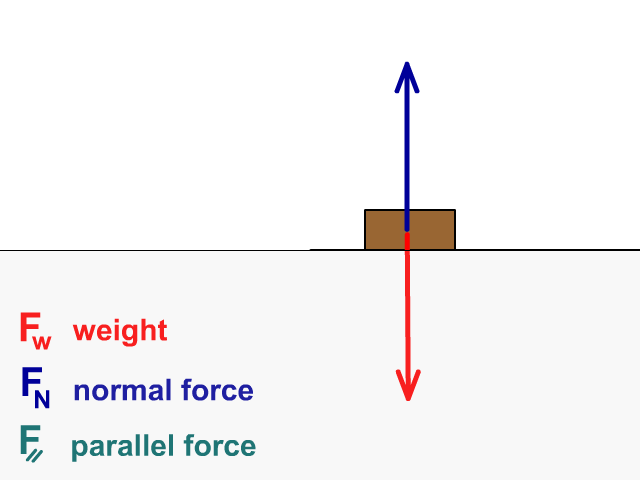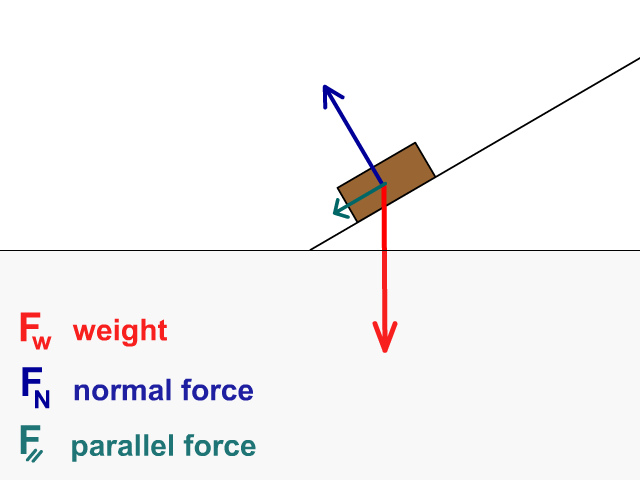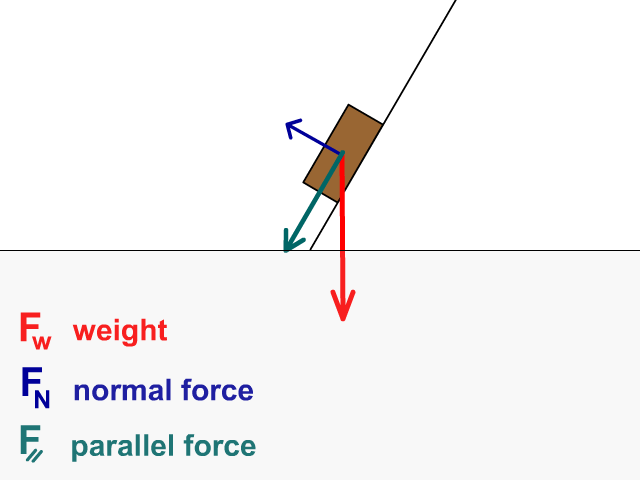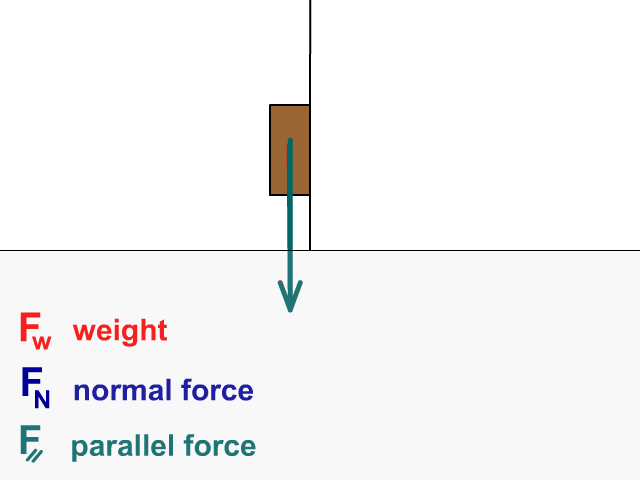
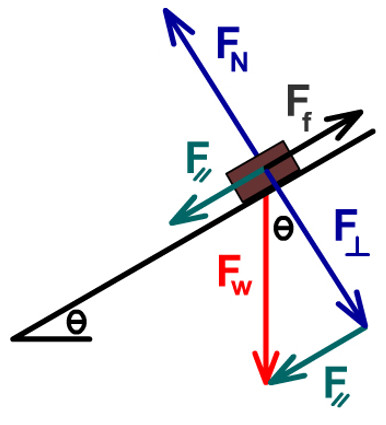
Forces on an incline

  • Fw: Weight
    • Longest Vector Straight Down
    • Some diagrams may use the variable Fg or mg in place of Fw

Other Real Forces

  • FN : Normal Force
    • Reaction to the force pushing into the hill (F⟘)and equal and opposite to it
  • Ff : Force of Friction
    • Reaction to the force pushing down the hill (F⸗ )

Other Component (Phantom) Forces

  • F⟘ : Perpendicular Force
    • Force pushing into the hill
  • F⸗ : Parallel Force
    • Force pushing down the hill

Other Symbols

  • Ө : Angle of Incline
    • Same as angle in the right triangle
Incline Plane

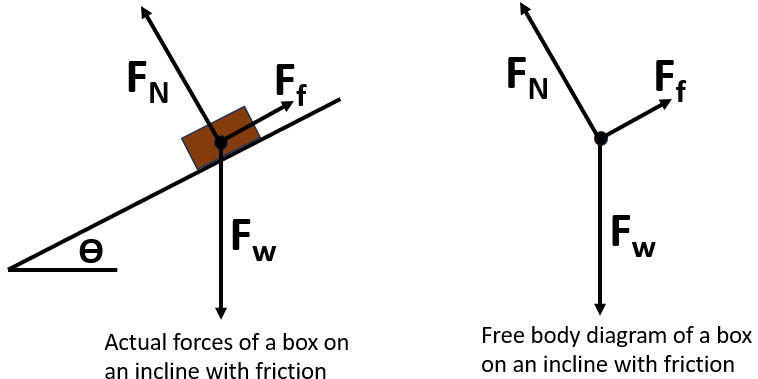
AP Physics Note:

If asked to draw a force diagram, do not include component also called phantom forces.  Component forces are part of a real force present and not themselves forces.  Weight is a real force and a component of weight is pushing into the hill and down the hill.  Components are important to solve problems but not to be included in an actual force diagram if asked to draw one for an exam.

Force diagram of a box on a hill

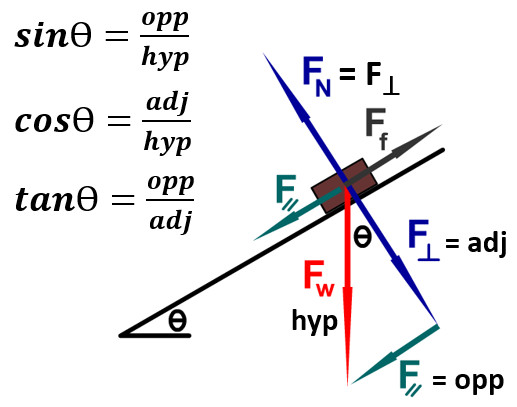
Incline Planes and Trig Functions

Depending what the incline plane question is asking you will use the SOH CAH TOA trig functions.  The most common case will be when you are given a mass on a hill and provided the hills incline(Ө).  Start by finding weight (FW = mg (g = 10 m/s2).  Because you have weight and an incline angle, you now can find other forces involved.  These are the most common rearranged forms.

  • F⟘ = (cosӨ)(hyp)
  • F⸗ = (sinӨ)(hyp)
  • FN = F⟘ = (cosӨ)(hyp)

Depending on how a the questions is asked you may need any of the trig functions including tangent.

incline and trig functions

What happens to forces as the incline increases?

  • Weight (FW) stays the same
  • Normal force (FN) decreases
  • Parallel force (F ⸗) increases
Increasing Angle of Incline

Q1: What other vector is the parallel force equal to if the incline was 90°?

Weight FW

Q2: Why would friction decrease as the angle of incline increases?

The coefficient of friction between two surface stays the same while normal force decreases

Ff = µFN

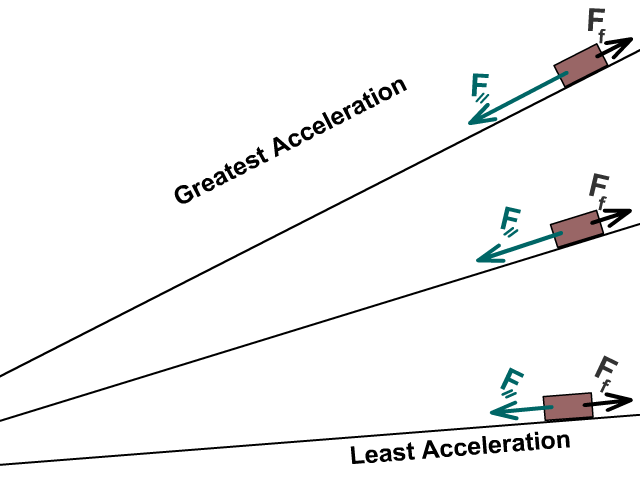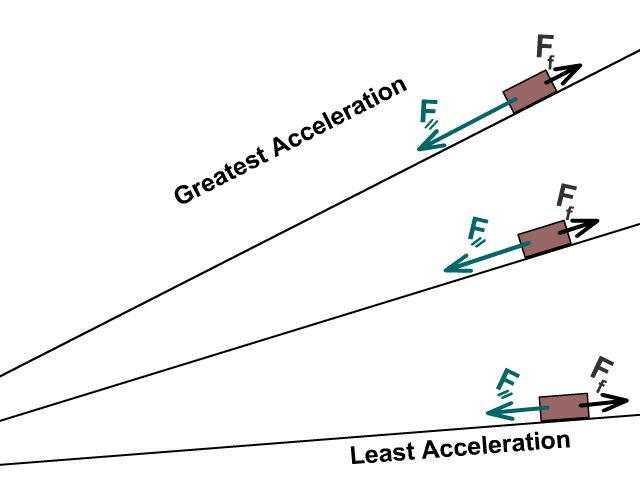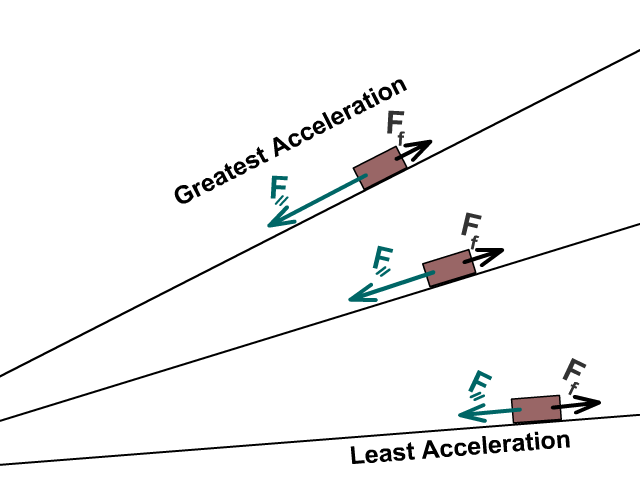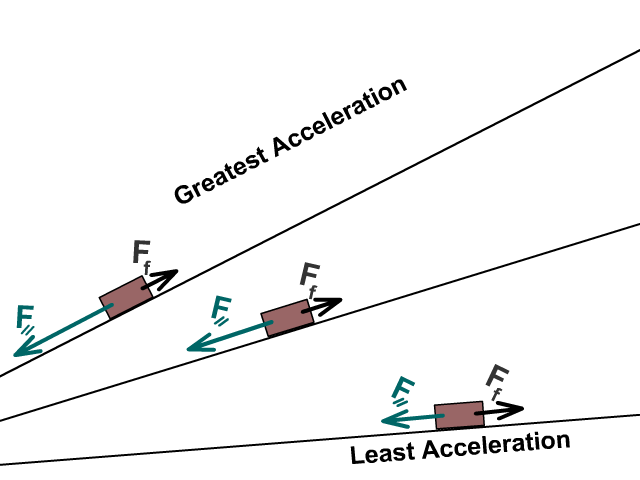
What happens to acceleration as the incline increases?

As an incline angle increases parallel force increases while frictional force decreases as a result of normal force going down.

Fnet = F⸗ – Ff

Net force and acceleration increase as the angle increases

Increased incline and acceleration

Solving for forces on an incline

Weight

FW = (mg)

hyp = (mg)

Perpendicular Force

F⟘ = (cosӨ)(hyp)

F⟘ = (cosӨ)(FW)

F⟘ = (cosӨ)(mg)

Parallel Force (Downhill Force)

F⸗ = (sinӨ)(hyp)

F⸗ = (sinӨ)(FW)

F⸗ = (sinӨ)(mg)

Normal Force

FN = F⟘ = (cosӨ)(hyp)

FN = (cosӨ)(FW)

FN = (cosӨ)(mg)

Solving for forces on an incline

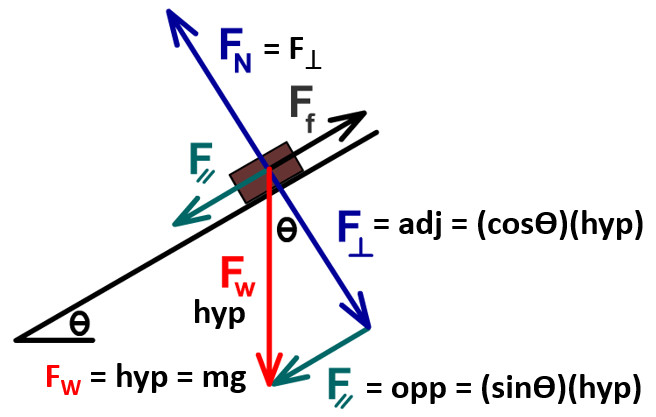
Net Force (Fnet) on a frictionless incline and no applied force

  • Net force comes completely from parallel force on a frictionless surface causing acceleration
  • F⸗ = Fnet
  • Fnet = ma

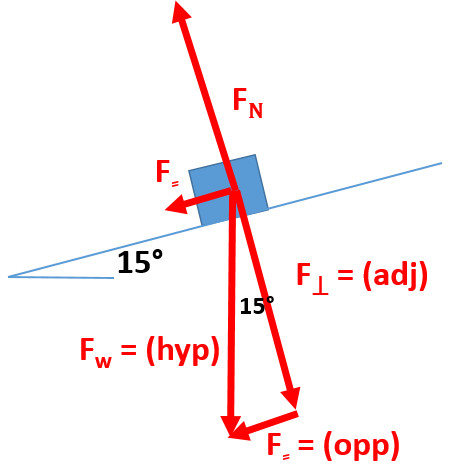
Finding downhill acceleration (Frictionless)

Fw = (mg)

hyp = (mg)

Find the parallel force substituting (mg) for the hypotenuse which is weight

F⸗ = opp = (sinӨ)(hyp)

F⸗ = (sinӨ)(mg)

The parallel force is the net force so we combine equations

F⸗ = Fnet

Fnet = (sinӨ)(mg)

Fnet = ma

a = ((sinӨ)(mg))/m

m cancels out resulting in an equation to solve for acceleration on an incline with only the angle of incline and acceleration due to gravity (g)

a = (sinӨ)(g)

 

Equation for solving for acceleration on an incline without friction:

a = (sinӨ)(g)

Questions

A 1.5 kg block is on a 15° frictionless incline plane

Q3: What is the normal force?

FN = (cosӨ)(mg)

FN = (cos15)(1.5)(10)

FN = 14.49 N

Q4: What is the force downhill?

F⸗ = (sinӨ)(mg)

F⸗ = (sin15)(1.5)(10)

F⸗ = 3.88 N downhill

Q5: What is the acceleration?

a = sin (Ө)(g)

a = sin (15)(10)

a = 2.59 m/s2 downhill

Alternative solution

Fnet = ma

a = (Fnet)/m

a = (3.88 N)/1.5

a = 2.59 m/s2 downhill

Force Diagram

Net Force (Fnet) with friction on an incline and no applied force

Parallel force minus friction is the net force creating acceleration

Use the parallel force downhill

F⸗ = (sinӨ)(mg)

Find friction substituting normal force

Ff = µFN

FN = (cosӨ)(mg)

Ff = µ (cosӨ)(mg)

Net force is the parallel force down the hill minus the force of friction uphill

Fnet = F⸗ - Ff

Fnet = (sinӨ)(mg) - µ (cosӨ)(mg)

Force diagram on an incline with friction

Finding downhill acceleration (with friction)

Fnet = ma

a = ((sinӨ)(mg) - µ (cosӨ)(mg))/m

You then cancel out the mass from the numerator and denominator

a = ((sinӨ)(g) - µ (cosӨ)(g))

which becomes a = (g)((sinӨ) - µ (cosӨ))

 

Equation for solving for acceleration on an incline with friction:

a = (g)((sinӨ) - µ (cosӨ))

Questions

A 5.3 kg block is on a 25° incline plane with a coefficient of static friction of 0.25 and coefficient of kinetic friction of 0.20

Q4: What is the normal force?

FN = (cosӨ)(mg)

FN = (cos25)(5.3)(10)

FN = 48.0 N

Q5: What is the force downhill?

F⸗ = (sinӨ)(mg)

F⸗ = (sin25)(5.3)(10)

F⸗ = 22.4 N downhill

Force Diagram 25 degree incline

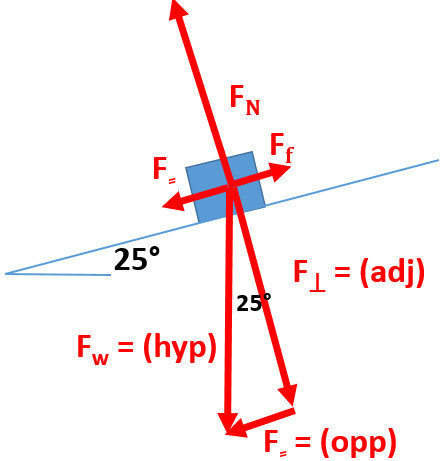
Q6: What is the force of static friction?

Ff = µFN

FN = (cosӨ)(mg)

Ff = µ (cosӨ)(mg)

Ff = (0.25)(cos25)(5.3)(10)

Ff = 12.0 N uphill

Q7: What is the force of kinetic friction?

Ff = µ (cosӨ)(mg)

Ff = (0.2)(cos25)(5.3)(10)

Ff = 9.6 N uphill

Q8: Would the block be moving?

Yes

The force downhill is more than the frictional force uphill

Ff = 12.0 N

F⸗ = 22.4 N

Q9: What is the net force on the block?

Ff = 9. N    (be sure to use the force of kinetic friction)

F⸗ = 22.4 N

Fnet = F⸗ - Ff

Fnet = 22.4 – 9.6    

Fnet = 12.8 N downhill

Q10: What is the block’s acceleration?

a = g((sinӨ)-µ(cosӨ))

a = (10)((sin25)-(0.2)(cos25))

a = 2.41 m/s2 downhill

another solution (only different due to rounding)

Fnet = ma

a = (Fnet)/m

a = (12.8)/5.3

a = 2.42 m/s2 downhill

Q11: How fast would the block be moving when starting from 2 m/s after 5 seconds?

Givens and unknown

vf = ?

a = 2.41 m/s2

vi = 2 m/s

t = 5 seconds

Equation and Work

vf = vi + at

vf = 2 + (2.41)(5)

Answer

vf = 14.05 m/s

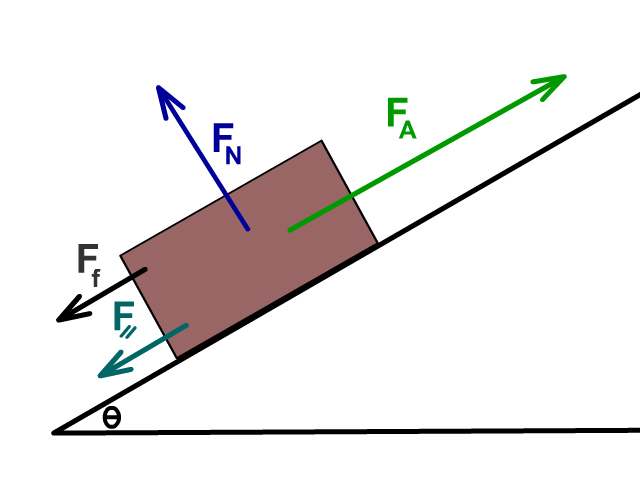
When a force is applied uphill on an incline

When a force is applied uphill on an incline

Friction will be downhill if motion is uphill

Net Force

Fnet = FA -  (F⸗ + Ff)

Fnet = FA -  ((sinӨ)(mg) + µ (cosӨ)(mg))

Acceleration

a =Fnet /m

Force applied uphill on an incline plane

When a force is applied downhill on an incline

Friction will be uphill if motion is downhill

Net Force

Fnet = (FA + F⸗) - Ff

Fnet = (FA + (sinӨ)(mg)) - µ (cosӨ)(mg)

Acceleration

a =Fnet /m

Force applied downhill on an incline plane

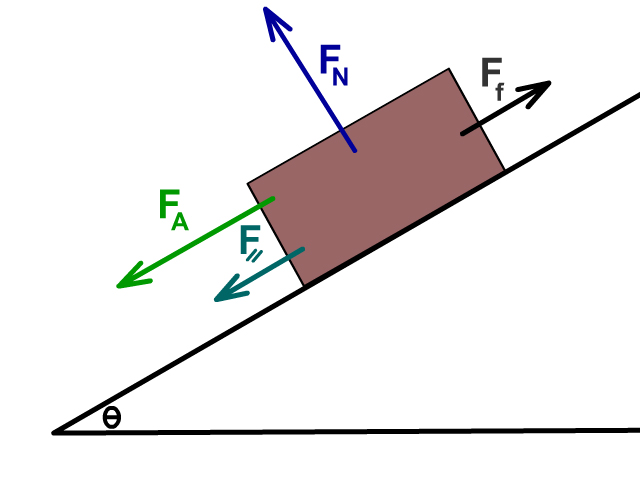
Sam pulls a 30 kg box up a 19° incline that has a coefficient of friction of 0.20 with a force of 200 N

Q12: What is the net force?

Fnet = FA -  ((sinӨ)(mg) + µ (cosӨ)(mg))

Fnet = 200 -  ((sin19)(30)(10)) + ((0.2)(cos19)(30)(10))

Fnet = 45.6 N Uphill

Q13: What is the acceleration?

a = Fnet/m

a = 45.6/30

a = 1.52 m/s2

Incline Plane Quiz

1 / 13

Incline Question Pic

Which letter above represents weight?

2 / 13

Incline Question Pic

Which letter above represents the parallel force?

3 / 13

Incline Question Pic

Which letter above represents normal force?

4 / 13

Incline Question Pic

Which letter above represents friction?

5 / 13

Incline Question Pic

Which number above is where the incline angle would be placed?

6 / 13

What happens to the normal force as the angle of incline increases?

7 / 13

What happens to the downhill force as the angle of incline increases?

8 / 13

What happens to the frictional force as the angle of incline increases?

9 / 13

What is the weight of a 4.0 kg object on a 25° frictionless Incline Plane? (Use g = 9.8 m/s2)

10 / 13

What is the acceleration of a moving object on a 4.0 kg object on a 25° Incline Plane that has a coefficient of friction with the object of 0.43?

11 / 13

What is the Normal force on a 4.0 kg object on a 25° Incline Plane?

12 / 13

What is the downhill force on a 4.0 kg object on a 25° Incline Plane?

13 / 13

What is the frictional force of a moving object on a 4.0 kg object on a 25° frictionless Incline Plane that has a coefficient of friction with the object of 0.43?

Your score is

LinkedIn Facebook Twitter
0%

Links

Terms and Conditions - Privacy Policy