Density of Fluids Practice Problem Set

Test your understanding of fluid density with our Density of Fluids Practice page! This page features multiple-choice questions, ranking tasks, and graphical analysis to help you explore the relationship between mass, volume, and density using standard physics units—kilograms (kg), cubic meters (m³), and kilograms per cubic meter (kg/m³). Refer to our Density of Fluids page for explanations and problem-solving tips.

Density of Fluids Practice Problem Set Section 1: Multiple-Choice Problems

Question 1:

A liquid has a mass of 4 kg and a volume of 0.004 m³. What is its density?

A) 2,500 kg/m³

B) 500 kg/m³

C) 1,000 kg/m³

D) 10,000 kg/m³

Answer: C) 1,000 kg/m³

Reasoning: Density = Mass ÷ Volume = 4 kg÷0.004 m³=1,000 kg/m³.

Question 2:

A block of metal has a density of 7,800 kg/m³ and a volume of 0.002 m³. What is its mass?

A) 15.6 kg

B) 7.8 kg

C) 1.56 kg

D) 780 kg

Answer: A) 15.6 kg

Reasoning: Mass = Density × Volume = 7,800 kg/m³×0.002 m³=15.6 kg

Question 3:

A fluid has a density of 900 kg/m³ and a mass of 2.7 kg. What is its volume?

A) 0.0042 m³

B) 0.030 m³

C) 0.0025 m³

D) 0.003 m³

Answer: D) 0.003 m³

Reasoning: Volume = Mass ÷ Density = 2.7 kg÷900 kg/m³=0.003 m³

Question 4:

Which of the following substances is most likely to float in water (density = 1,000 kg/m³)?

A) Substance A: 1,500 kg/m³

B) Substance B: 800 kg/m³

C) Substance C: 1,200 kg/m³

D) Substance D: 2,000 kg/m³

Answer: B) 800 kg/m³

Reasoning: Substances with a density less than 1,000 kg/m³ float in water.

Question 5:

What happens to the density of a liquid when its temperature increases?

A) Density increases.

B) Density decreases.

C) Density remains constant.

D) It depends on the liquid.

Answer: B) Density decreases.

Reasoning: When temperature increases, the liquid expands, this increases volume while mass remains unchanged decreasing its density.

Density of Fluids Practice Problem Set Section 2: Ranking Tasks

Question 6:

Rank the following materials by density from lowest to highest:

Ethanol: 790 kg/m³
Glycerin: 1,260 kg/m³
Ice: 920 kg/m³
Water: 1,000 kg/m³

Answer: Ethanol < Ice < Water < Glycerin

Reasoning: Compare each material’s density in kg/m³ and arrange them in ascending order.

Question 7:

Arrange these blocks by their sinking speed in water, assuming equal volumes:

Copper: 8,960 kg/m³
Lead: 11,340 kg/m³
Steel: 7,850 kg/m³
Aluminum: 2,700 kg/m³

Answer: Lead > Copper > Steel > Aluminum

Reasoning: Higher density causes faster sinking, assuming equal volumes.

Question 8:

Rank these liquids by their likelihood of floating on water:

Honey: 1,420 kg/m³
Vegetable oil: 920 kg/m³
Seawater: 1,025 kg/m³
Rubbing alcohol: 785 kg/m³

Answer: Rubbing alcohol > Vegetable oil > Seawater > Honey

Reasoning: Substances with lower densities are more likely to float.

Question 9:

The table below shows the mass and volume for four mystery solutions. Rank the solutions from highest to lowest density.

Solution	Mass (kg)	Volume (m³)
Solution A	4.5	0.003
Solution B	3.6	0.004
Solution C	5.4	0.003
Solution D	4.2	0.005

Answer: Solution C > Solution A > Solution B > Solution D

Explanation: To calculate density:

Solution A: 4.5 ÷ 0.003 = 1,500 kg/m³
Solution B: 3.6 ÷ 0.004 = 900 kg/m³
Solution C: 5.4 ÷ 0.003 = 1,800 kg/m³
Solution D: 4.2 ÷ 0.005 = 840 kg/m³

The ranking is based on these calculated densities.

Question 10:

The table below shows the mass and volume for another set of mystery solutions. Rank the solutions from highest to lowest density.

Solution	Mass (kg)	Volume (m³)
Solution E	6.0	0.004
Solution F	7.2	0.005
Solution G	8.0	0.006
Solution H	5.4	0.003

Answer: Solution H > Solution E > Solution F > Solution G

Explanation: To calculate density:

Solution E: 6.0÷0.004=1,500 kg/m³
Solution F: 7.2÷0.005=1,440 kg/m³
Solution G: 8.0÷0.006=1,333 kg/m³
Solution H: 5.4÷0.003=1,800 kg/m³

The ranking is based on these calculated densities.

Practice Section 3: Data Analysis

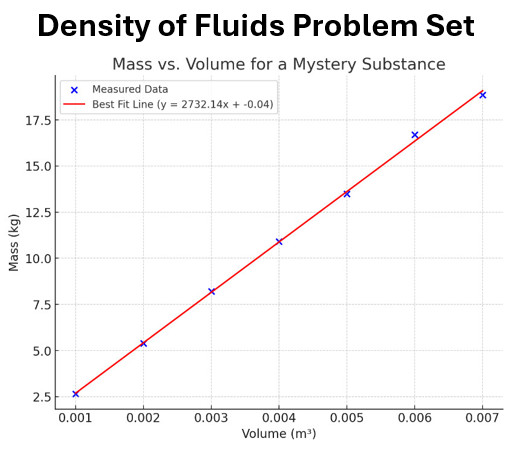
Lab Data for a Mystery Substance

The table and graph below represent data collected by students during a lab experiment to analyze a mystery substance.

Volume (m³)	Mass (kg)
0.001	2.650
0.002	5.400
0.003	8.200
0.004	10.900
0.005	13.500
0.006	16.700
0.007	18.850

Mass vs Volume for Density Calculations of a Mystery Fluid

Best Fit Line Lab Data Question

Question 11: Use the table and graph at the beginning of this section to answer the question

What is the density of the mystery substance based on the best-fit line?

A) 2,700 kg/m³

B) 2,650 kg/m³

C) 2,500 kg/m³

D) 3,000 kg/m³

Answer: A) 2,700 kg/m³

Reasoning:
The slope of the best-fit line represents the density of the substance because density is defined as the ratio of mass to volume:

Instead of using raw data points, which may include small experimental errors, we use points directly from the best-fit line. This ensures a more accurate calculation of the density by reducing the influence of individual measurement inaccuracies.

From the best-fit line on the graph, select two points:

At Volume = 0.002 m³, the corresponding Mass = 5.4 kg

At Volume = 0.006 m³, the corresponding Mass = 16.2 kg

The slope of a line is calculated as the ratio of the rise (change in mass) to the run (change in volume):

Substituting the values for the rise (ΔMass) and run (ΔVolume):

Now calculate the slope:

Thus, the density of the substance, based on the best-fit line, is 2,700 kg/m³. This method ensures greater accuracy by relying on the trend indicated by the best-fit line rather than individual data points, which may include minor errors.

Conclusion

The Density of Fluids Practice shows how mass, volume, and density are connected. Use this page to revisit problems and data analysis whenever you need to refresh your understanding of fluid density.