Fluids are everywhere: in the oceans, the atmosphere, and even inside our bodies. Understanding their behavior begins with the foundational concept of density. This lesson will explore what density means, its equation, and its application to fluids, giving you a solid understanding of this critical property.
Test Your Knowledge of Density
Before diving deeper into the concept of density, why not test what you already know? Visit our Density of Fluids Practice page to solve real-world problems and see how well you understand the basics. Then, revisit it after the lesson to reinforce what you’ve learned!

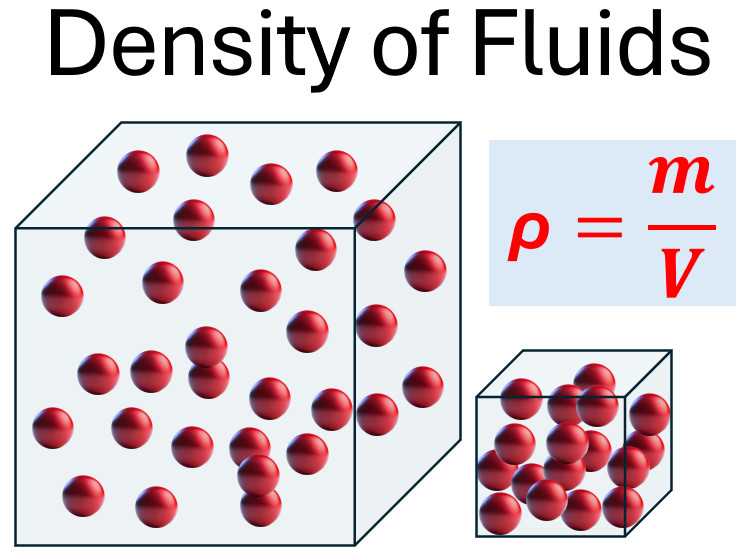
To understand the concept of density, it is essential to first grasp mass and volume. Mass represents the amount of matter within an object, while volume refers to the space the object occupies. Together, these properties determine an object’s density. This picture visually ties these ideas together by showing how varying mass and volume affect density. The larger cube demonstrates a scenario with more mass, more volume, and lower density. By observing this relationship, the role of mass and volume in defining density becomes clearer.
More vs. Less Mass

This picture shows the concept of mass with identical particles. On the left, “More Mass” features a greater number of identical red particles, indicating a higher quantity of matter. On the right, “Less Mass” displays fewer particles, reflecting a lower quantity of matter. The number of particles portrays the mass difference, as all particles share the same size and composition. However, when the particles differ in mass, the comparison becomes more complex. In such cases, larger particles contribute more mass than smaller or less dense ones, thereby altering the relationship between the number of particles and the total mass.
More vs. Less Volume

The picture illustrates the concept of volume through two cubes. The left cube represents “More Volume” with larger dimensions, while the right cube shows “Less Volume” with smaller dimensions. The volume of a cube depends on the length of its sides, calculated using the formula V=s3, where s represents the side length. A larger side length results in a significantly greater volume, as shown by the larger cube in the image.
Higher vs. Lower Density

This picture illustrates the concept of density which includes both mass and volume. The cube on the left, labeled “Higher Density,” contains a larger number of spheres packed closely together, representing a higher density. The cube on the right, labeled “Lower Density,” has fewer spheres spaced farther apart.
This image relates to the prior one by combining the concepts of mass and volume to explain density.
What is Density?
Density (ρ, pronounced “rho”) is a measure of how much mass is packed into a given volume. It tells us how “heavy” or “light” a material is relative to its size. In physics, density is defined by the equation:
ρ = m / V
Where:
- ρ (rho) = density (measured in kilograms per cubic meter, kg/m³, in the SI system)
- m = mass (measured in kilograms, kg)
- V = volume (measured in cubic meters, m³)
This simple equation reveals a lot about a substance. For instance, a high-density material like lead has a significant amount of mass packed into a small volume. Lead, with a density of approximately 11,340 kg/m³, contains 11,340 kilograms of mass in every cubic meter. Therefore, it ranks as one of the densest commonly encountered materials. As a result, lead is ideal for applications requiring heavy and compact materials, such as radiation shielding or ballast weights.
Conversely, a low-density material like air has relatively little mass within the same volume. Air, with a density of around 1.225 kg/m³ at sea level under standard conditions, is much lighter. This low density makes air easily compressible and explains why balloons rise when filled with lighter gases like helium (density 0.1785 kg/m³).
Table of Densities
Here is a table of six well-known substances for each state of matter—solids, liquids, and gases—along with their densities:
| Substance | State | Density (kg/m³) |
|---|---|---|
| Aluminum | Solid | 2,700 |
| Iron | Solid | 7,870 |
| Copper | Solid | 8,940 |
| Silver | Solid | 10,500 |
| Lead | Solid | 11,340 |
| Gold | Solid | 19,320 |
| Water | Liquid | 1,000 |
| Ethanol | Liquid | 789 |
| Olive Oil | Liquid | 910 |
| Glycerin | Liquid | 1,261 |
| Mercury | Liquid | 13,546 |
| Acetone | Liquid | 784 |
| Hydrogen | Gas | 0.0898 |
| Helium | Gas | 0.179 |
| Air | Gas | 1.2 |
| Carbon Dioxide | Gas | 1.98 |
| Methane | Gas | 0.668 |
| Neon | Gas | 0.9 |
These values are sourced from the Wikipedia: Density page. For more detailed information and additional substances, please refer to the provided link.
Deriving Density: A Practical Approach
Imagine you have a block of material with a mass of 12 kg and a volume of 3 m³. Using the density formula:
ρ = m / V
ρ = 12 kg / 3 m³
ρ = 4 kg/m³
This result tells us that every cubic meter of the material contains 4 kg of mass. By contrast, water has a standard density of 1,000 kg/m³ at room temperature. Comparing these values helps us understand whether a material will float or sink when placed in water—a critical concept in fluid mechanics.
Density in Fluids
In fluids, density can vary depending on:
- Composition: Saltwater, for example, is denser than freshwater because dissolved salts increase mass without significantly increasing volume.
- Temperature: As temperature increases, most fluids expand, increasing their volume and decreasing their density.
- Pressure: At high pressures, fluids compress slightly, decreasing their volume and increasing their density, which means the particles are forced closer together.
Note: In our discussion of fluids, we will focus on incompressible or ideal fluids. This assumption simplifies calculations by treating density as constant, allowing for a clearer understanding of core fluid principles.
Measuring Density of Fluids
To measure the density of a fluid, you can use:
- Mass Measurement: Use a balance or scale to determine the fluid’s mass.
- Volume Measurement: Use a graduated cylinder, pipette, or displacement method for irregular shapes.
Simple Experiment Example: Measuring Water Density
- Measure 1 liter (0.001 m³) of water.
- Determine its mass (typically around 1 kg at room temperature).
- Calculate density:
ρ = m / V
ρ = 1 kg / 0.001 m³ = 1,000 kg/m³
This method provides a straightforward way to calculate density, but it relies on a single measurement. A better approach involves multiple measurements to reduce error and improve accuracy.
Reducing Error in Density of Fluid Measurements
One way to improve the accuracy of density measurements is by using multiple mass and volume measurements instead of relying on a single measurement. By graphing these values and analyzing the data, we can reduce the impact of measurement errors.
Here’s how:
- Measure the mass of a substance multiple times, each time with a different volume. For example, you can use graduated cylinders to measure several distinct fluid volumes (e.g., 50 mL, 100 mL, 150 mL, 200 mL, 250 mL, 300 mL). Note: 1 mL of water equals 0.000001 m³. This conversion is useful when working with smaller volumes in laboratory settings.
- Record the corresponding masses for each volume using a precision balance.
- Plot the data on a graph with volume (V) on the x-axis and mass (m) on the y-axis.
- Draw the best-fit line through the data points using a ruler or software.
| Lab Data For Mass And Volume | |
| Volume (m3) | Mass (kg) |
| 0.00005 | 0.505 |
| 0.00010 | 0.1012 |
| 0.00015 | 0.1498 |
| 0.00020 | 0.2003 |
| 0.00025 | 0.2495 |
| 0.00030 | 0.3021 |

The density equation (ρ = m/V) transforms into the equation of the slope of a line (y = mx + b), or simply (y = mx) since zero volume correlates with zero mass. Therefore, this relationship simplifies to m=ρV.
Because m represents both mass and slope, I explicitly labeled slope in the picture while keeping mass as m.
When volume appears on the X-axis and mass on the Y-axis, the slope of the best-fit line now represents density (ρ).

Why Graphing Improves Accuracy
When you use only one mass and one volume measurement to calculate density, errors can directly affect the result. Therefore, taking multiple measurements and plotting them on a graph provides a better solution. By carefully analyzing the slope of a best-fit line, this method averages out individual errors and produces a more reliable density value. As a result, it becomes especially useful in experimental setups prone to small but significant uncertainties.
For instance, in earlier data points, calculating density with a single mass of 0.1012 kg and a volume of 0.0001 m³ yields 1,012.00 kg/m³. However, this value significantly deviates from water’s actual density at room temperature, approximately 1,000 kg/m³. In contrast, the best-fit line calculation of 1,001.94 kg/m³ aligns much closer to the true value. Clearly, this approach demonstrates how graphing minimizes the impact of individual measurement errors while significantly improving overall accuracy.
Density of Fluids Physics Applications
1. Floating and Sinking
An object placed in a fluid will:
- Float if its density is less than the fluid’s density.
- Sink if its density is greater than the fluid’s density.
For example, wood (ρ ≈ 700 kg/m³) floats in water, while steel (ρ ≈ 7,800 kg/m³) sinks unless shaped into a hollow structure like a ship.
2. Fluid Layers
In a container, fluids with different densities naturally form layers, with the densest fluid settling at the bottom. This principle is crucial in fields like oceanography and meteorology.
3. Engineering and Design
Knowing the density of materials allows engineers to:
- Design ships and submarines that float or submerge as needed.
- Construct buildings that can withstand specific fluid forces like wind or water pressure.
Advanced Considerations: Density of Fluids and Specific Gravity
Specific gravity is a related concept that compares the density of a fluid to a reference substance, typically water:
Specific Gravity = ρsubstance/ρwater
For water at 4°C (standard conditions), ρwater = 1,000 kg/m³. Substances with a specific gravity:
- >1 are denser than water and sink.
- <1 are less dense and float.
Real-World Example: Oil Spills
When oil leaks into the ocean, it floats on water because its density (≈ 920 kg/m³) is lower than seawater’s density (≈ 1,025 kg/m³). Consequently, this density difference allows environmental engineers to design effective cleanup methods using buoyancy principles.
Density of Fluids Recap
- Density (ρ = m/V) measures how much mass is packed into a volume.
- Factors like composition, temperature, and pressure affect fluid density.
- Density plays a key role in phenomena like buoyancy, layering, and material design.
Ready to Test Your Skills?
Put your knowledge to the test with our Density of Fluids Practice page! Solve real-world problems, rank substances by density, and analyze graphical data to reinforce what you’ve learned. It’s the perfect way to apply your understanding and master the concept of fluid density.
Density of Fluids Conclusion
Understanding the density of fluids is the first step in mastering fluid mechanics. With this foundational knowledge, you’re ready to explore more complex fluid behaviors like pressure, buoyant force, and fluid dynamics. Ready to dive deeper? The next lesson, Pressure in Fluids: Exploring P = F/A and Depth Factors, builds on this concept. Let’s keep learning!