Solving for Components in Physics
Understanding components is absolutely essential when solving physics problems involving vectors, such as projectile motion, inclined planes, and forces applied at angles. To help clarify this important topic, this article thoroughly explores the concept of solving for components in physics, clearly explains why they are necessary, and provides detailed examples to illustrate their importance. Furthermore, it highlights how mastering this critical skill can significantly simplify complex problems and, in turn, improve overall problem-solving efficiency.
Why Solving for Components Is Needed
In physics, vectors represent quantities such as velocity, force, or displacement, which have both magnitude and direction. Therefore, to solve problems involving vectors, we often break them into their x (horizontal) and y (vertical) components. By doing so, we simplify complex motions into more manageable parts. This approach is particularly useful when forces or motions act independently along these axes, allowing for more precise calculations.
Example 1: Projectile Motion

Consider a soccer player kicking a ball with an initial velocity of 36 m/s at an angle of 30 degrees to the ground. Solving for components is critical because:
The y-axis component of velocity represents vertical motion, which is influenced by gravity, causing the ball to accelerate downward at 9.8 m/s2.
The x-axis component of velocity represents horizontal motion, which remains constant as gravity does not affect it.
Using Trigonometry (SOH CAH TOA):
- SOH CAH TOA is a mnemonic for the trigonometric functions: sinƟ=opp/hyp, cosƟ=adj/hyp, and tanƟ=opp/adj. This serves as a starting point for solving for components.
The initial vertical component of velocity (vY) uses opp=(sinƟ)(hyp) specialized for velocity as vY=(sinƟ)(v) where v is the original velocity of the kick at an angle. Substituting values:
vY = (sinƟ)(v) = sin30(36) = 18 m/s vertically
The initial horizontal component of velocity (vX) uses adj=(cosƟ)(hyp) specialized for velocity as vX=(cosƟ)(v) where v is the original velocity of the kick at an angle. Substituting values:
vX = (cosƟ)(v) = (cos30)(36) = 31.18 m/s horizontally
These components are the starting point for solving projectile motion problems, such as calculating range, time of flight, or maximum height. Explore projectile motion problems here.
Real-World Applications of Solving for Components
Example 2: Navigating Directions

Suppose a person is traveling 100 meters 50 degrees north of east. To determine how far north or east they traveled:
North component:
dY = (sinƟ)(d) = (sin50)(100) = 76.6 m north
East component:
dX = (cosƟ)(d) = (cos50)(100) = 64.3 m east
These calculations are crucial for applications like navigation in hiking, aviation, or tracking weather systems.
Learn more about components with example problems on this page linked here.
Example 3: Pulling a Wagon at an Angle

Imagine a person pulling a wagon with a force of 120 N at an angle of 25 degrees to the ground. Why is solving for components necessary?
The vertical component, (FY), reduces the normal force, which affects friction.
The horizontal component, (FX), is a major component of determining the force causing acceleration.
Upward Component:
FY = (sinƟ)(d) = (sin25)(120) = 50.7 N up
Forward Component:
FX = (cosƟ)(d) = (cos25)(120) = 108.8 N Forward
If the frictional force is 20 N, then the net force is 88.8 N. Importantly, the net force determines the wagon’s acceleration. In contrast, it is not the applied or horizontal force that affects acceleration. Furthermore, if you know the wagon’s mass and the coefficient of friction, you can calculate the frictional force yourself. For more clarity, see a full example of a similar problem here.
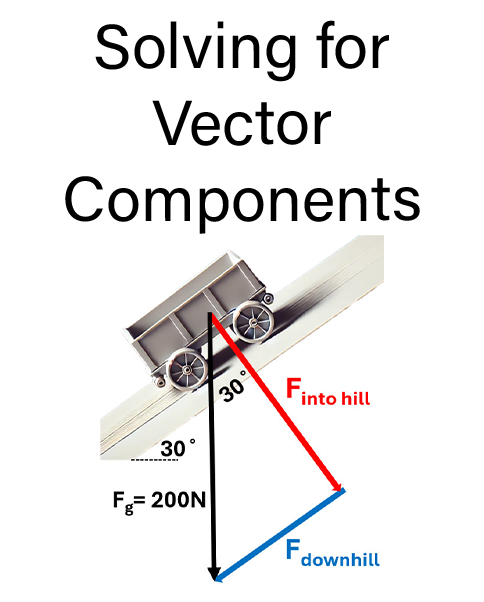
Example 4: Inclined Planes

On an incline, an object’s weight creates two components:
- Parallel force: Pulls the object downhill.
- Perpendicular force: Pushes into the hill, affecting the normal force and friction.
If the weight of the object is 200 N down and the incline of the hill is 30 degrees:
Parallel Downhill Component:
Fdownhill = (sinƟ)(F) = (sin30)(200) = 100 N downhill
Perpendicular Into Hill Component:
Finto hill = (cosƟ)(F) = (cos30)(200) = 173.2 N into hill
These components are critical for calculating friction and net force. Explore inclined plane problems here.
Why Solving for Components Matters
Breaking forces and motions into components is a powerful tool for physicists and engineers. This method allows us to:
- Analyze forces and motion in multiple dimensions.
- Simplify complex problems into manageable parts.
- Predict real-world behavior of objects with precision.
- Enhance the design of bridges, vehicles, and sports equipment.
A historical breakthrough: Galileo’s studies of motion in two dimensions laid the groundwork for modern physics and mechanics, making these analyses possible.
Additional Resources
For more physics insights, check out:
Mastering components is the first step to solving more complex problems. Once you’re ready, explore:
Applying Component Analysis to Real-World Physics
By solving for components, students can effectively break down complex scenarios into simpler parts, thereby paving the way for mastering advanced physics concepts. Moreover, whether they are analyzing projectile motion or designing efficient systems, component analysis serves as the foundation for accurate calculations and practical applications.