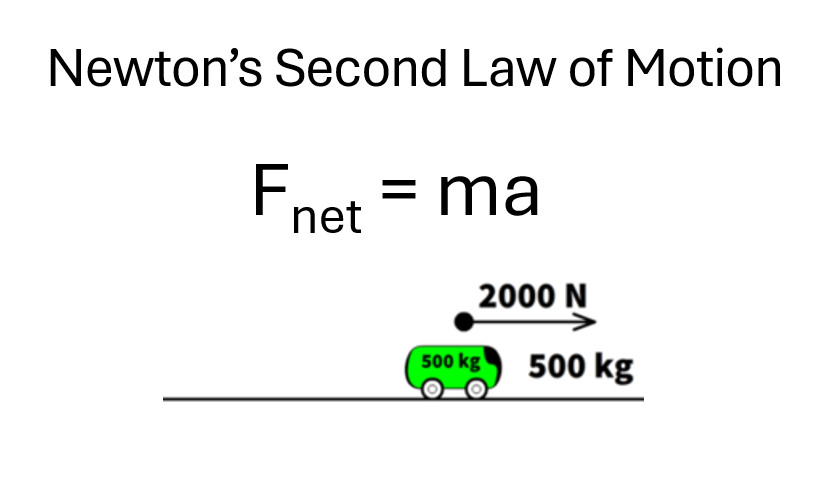
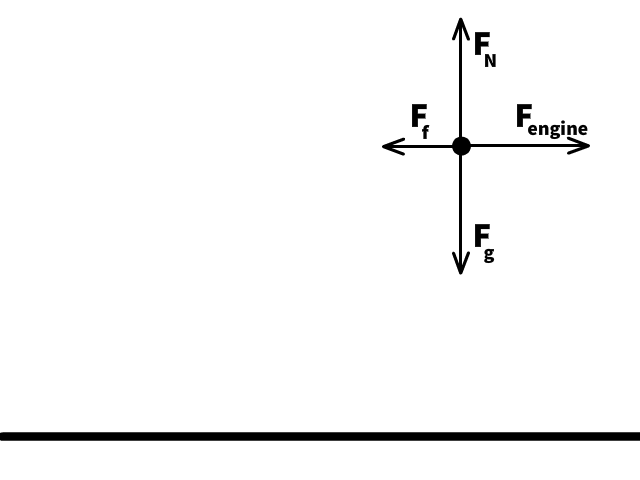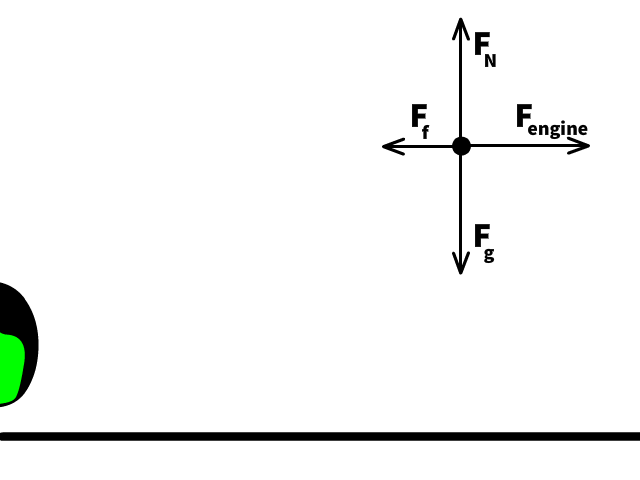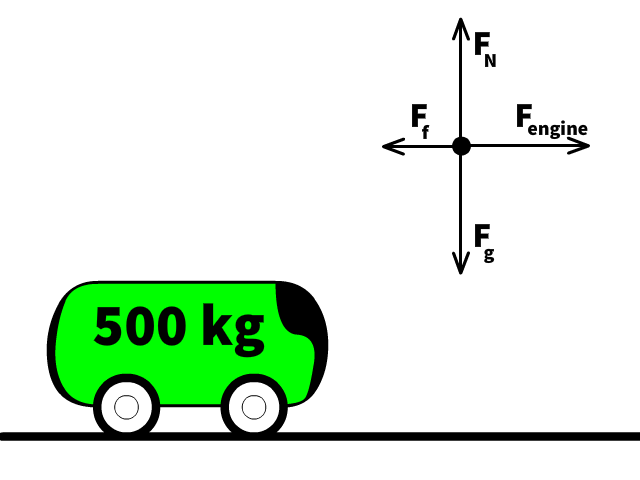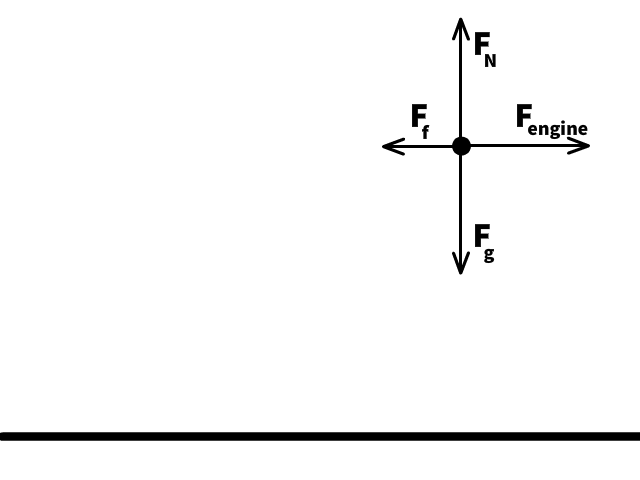
Newton’s Second Law of Motion, expressed as Fnet=ma, explains how force and mass influence acceleration. It is crucial for understanding how systems behave under unbalanced forces, especially when not in equilibrium.
What Happens When a System is Not in Equilibrium?
When an external net force acts on a system, it is no longer in equilibrium. This imbalance causes the center of mass of the system to accelerate. The acceleration depends on the magnitude of the net force and the system’s mass.
Newton’s Second Law: Fnet = ma
An unbalanced net force will create an acceleration. The amount of acceleration will depend on its mass.
Equation: Fnet = ma
Rearranged to analyze acceleration: 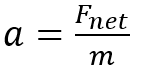
Using Newton’s Second Law to Determine Acceleration
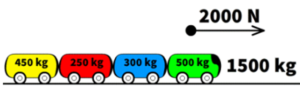
Let’s calculate the acceleration of the entire train using the 2000 Newtons of propulsion force from the green cart. To find acceleration, use a=Fnet/m, which requires dividing the 2000 N net force by the train’s total mass. Assuming a frictionless track, divide 2000 N by 1500 kg to complete the calculation. As a result, the train’s acceleration equals 1.33 m/s2.
If a frictional force was involved, we would have to start by figuring out a net force. To learn more about net force, visit our net force lesson on this page linked here.
Calculate Acceleration of the Green Cart Alone Using Newton’s Second Law
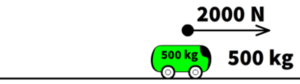


Now let’s calculate the acceleration of the green cart pulling only itself with its 2000 Newtons of propulsion force. Using a=Fnet/m, divide the 2000 N net force by the cart’s mass of 500 kg. Assuming a frictionless track, the calculation becomes a=2000/400, resulting in an acceleration of 4.0 m/s2.
Using Ratios to Understand Acceleration Changes with Increasing Mass in a Cart System
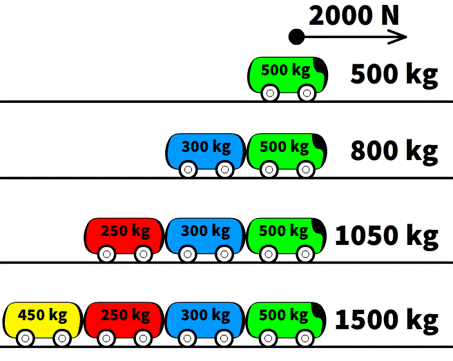
In this example, the net force remains constant at 1x the original of 2000 Newtons. However, the total mass of the system increases with each added cart. The green locomotive alone equals 1 times its original mass. When combined with the blue cart, the mass becomes 1.6 times the original. Adding the red cart increases the mass to 2.1 times, and including the yellow cart raises it to 3 times the original. For a reminder of how these ratios were calculated, refer to our Newton’s First Law of Motion page linked here. For a deeper dive or a refresher on ratios, check out this rule of ones explanation.

Solving Acceleration with Constant Force and Changing Mass Ratios
We can apply Newton’s Second Law of Motion to calculate the acceleration of the green cart pulling a system with added carts. In these examples, we know the actual amounts of force and mass involved. However, in some problems, we only know how a variable changes as a multiple or ratio. Rather than calculating the exact acceleration in meters per second squared, we focus on determining how many times the acceleration changes.
Using Ratios to Determine Acceleration Changes
Since a=Fnet/m, acceleration is determined by dividing the net force by the mass. To find the difference in acceleration, we set up a ratio of the new Fnet/m divided by the original Fnet/m.
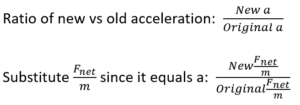
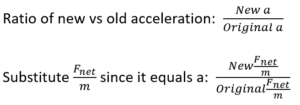
Understanding Multipliers in Ratio Problems
In ratio problems, we don’t use the actual force value of 2000 N but instead treat it as 1, representing one times the original force. Similarly, our baseline mass of 500 kg is referred to as 1, indicating one times the original mass. Any new mass is expressed as a multiplier, showing how many times greater it is compared to the baseline. These mass multipliers were calculated in our previous lesson for reference.
A) Green & Blue acceleration with 1.6 times the original mass and the same force applied
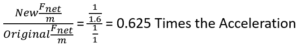
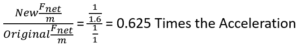
B) Green, Blue, and Red acceleration with 2.1 times the original mass and the same force applied
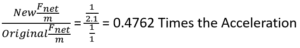
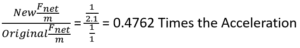
C) Green, Blue, Red and Yellow acceleration with 3 times the original mass and the same force applied
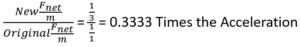
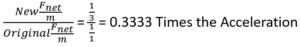
Verifying Acceleration Ratios with Newton’s Second Law
We already calculated the acceleration of the green cart pulling only itself earlier at 4.0 m/s2. Now, let’s calculate the acceleration of the green cart pulling a system with all the possible carts. Using the a=Fnet/m equation and actual numbers, we can confirm that our acceleration ratio calculations are accurate.



a = 2000/500 = 4 m/s2 Forward
What is the acceleration of the 800 kg green and blue cart train if the green engine applies 2000 N forward?
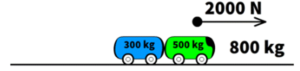

Using a ratio to solve this problem. We determined the ratio to 0.625 times the acceleration.
- (Green alone acceleration) x (acceleration ratio of green & blue)
- (4 m/s2)(0.625) = 2.5 m/s2 Forward
Using a direct calculation you would get the same result.
- a = Fnet/m
- a = 2000N/800kg
- a = 2.5 m/s2 Forward
Question: Determine the acceleration of the green engine pulling the green, red, and blue together.
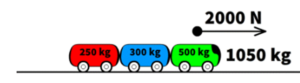

Question: Determine the acceleration of the green engine pulling the green, red, blue, and yellow together.



Here are the resulting differences in acceleration and what they would look like relatively when the green cart is pushing itself or a combination of multiple carts will less acceleration because of more mass and more inertia.


Conclusion: Newton’s Second Law of Motion
Newton’s Second Law of Motion links force, mass, and acceleration, helping us analyze motion directly or through ratios. By exploring examples like the green cart pulling systems of carts, we saw how changes in mass affect acceleration. These insights connect theory to real-world motion, building a foundation for advanced physics topics.
Learn more about Newton’s Law Watching this PBS Crash Course on Newton’s Laws of Motion here.