Understanding the interplay between momentum and energy in systems is fundamental in physics. This lesson explores how changes in momentum and mechanical energy can indicate the presence of external forces, offering insights into the dynamics of collisions, motion, and system interactions. By analyzing graphs and real-world scenarios, we uncover how forces shape the behavior of systems, whether closed or influenced by external factors.
What Are Momentum and Mechanical Energy?
Momentum (p=mv) is the product of an object’s mass and velocity, representing its “quantity of motion.” Mechanical energy encompasses various forms, including kinetic energy—such as linear kinetic energy (K = ½ mv2) and rotational kinetic energy (K=½I𝜔2)—and potential energy, such as gravitational potential energy (Ug=mgy) and elastic potential energy (Us=½kx2). While momentum and mechanical energy are distinct properties, their changes are intricately linked when external forces act on a system.
Momentum Conservation
In the absence of external forces, the total momentum of a system remains constant. The combined momentum of all objects within the system before an event, such as a collision or motion down a hill, will equal the total momentum afterward.
Energy Conservation
Similarly, mechanical energy is conserved unless external forces perform work on the system. The total mechanical energy of all objects in the system before an event, such as a collision or rolling down a hill, should equal the total mechanical energy afterward, provided no external forces like friction or air resistance are acting.
Identifying External Forces in Momentum and Energy Systems
Determining whether a system is influenced by external forces involves analyzing both momentum and energy changes.
Step 1: Define the System

Clearly identify the boundaries of your system and the objects within it. This distinction is crucial for assessing external influences and determining how forces impact the system. As a physics student, remember that the definition of the system may be provided in a Free Response Question (FRQ) or Multiple Choice Question (MCQ), and this definition can significantly affect how you approach and answer the problem.
The system can be as simple or as complex as the problem defines or you choose to analyze:
- Single Object: The system could include just one object, such as Car A. In this case, external forces like gravity, friction, or interaction with Car B must be considered.
- Multiple Objects: The system could include both Car A and Car B together, treating their interactions (e.g., a collision) as internal forces.
- Extended System: The system could also encompass additional forces, such as the Earth’s gravitational pull or friction between the cars and the ground, which might act as external forces altering the total momentum or mechanical energy of the system.
Carefully defining the system determines whether forces are internal (which cancel out) or external (which can change the total momentum or energy), impacting the solution and interpretation of the problem.
Step 2: Evaluate Internal Interactions
Internal forces, such as those in collisions, cause individual momentum changes. However, in a closed system, these changes cancel out, leaving the total momentum unchanged.
Example:
Two ice skaters push off each other:
- Skater A moves right (positive momentum change).
- Skater B moves left (negative momentum change).
- Result: The system’s total momentum remains unchanged.
Step 3: Look for Momentum and Energy Changes
If the system’s total momentum or mechanical energy changes, external forces are acting on it. For example:
- Friction reduces mechanical energy by converting it to heat.
- Gravity adds potential or kinetic energy to a system.
Graphs as Tools for Analysis
Graphs are vital for visualizing momentum and energy changes and identifying external forces.
Force-Time Graphs
- The area under a force-time graph represents impulse (J), which equals the change in momentum.
- If the net impulse is nonzero, an external force acted on the system.
Lets consider the situation of two cars colliding. As systems of individual carts and then as a whole.
Initially the cars were rolling each with their own momentums until the collision occurred.
We will call right positive and left negative in our examples.
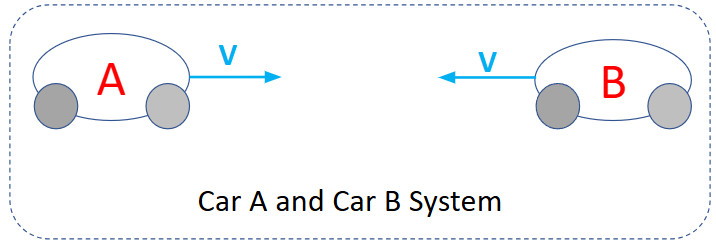
Impulse on the Car A system
Car A experiences a force of -2N (negative because it acts to the left) for 0.3 s. The resulting impulse on Car A is:
J=F⋅Δt=(−2⋅0.3 )=-0.6 N·s
This impulse causes a change in momentum of -0.6 kg·m/s or 0.6 kg·m/s to the left. Whatever Car A’s momentum was before the force acted, it has now changed by this amount.

Impulse on the Car B System
Car B experiences a force of 2N to the right for 0.3 s. The resulting impulse on Car B is:
J=F⋅Δt=(2⋅0.3 )=0.6 N·s
This impulse causes a change in momentum of 0.6 kg·m/s to the right. Whatever Car B’s momentum was before the force acted, it has now changed by this amount.

Impulse on the Car A-B System
Since all the forces were internal to the two cart system, there was no external impulse and therefore no resulting change in momentum from the initial momentum of the system. This alone does not show the momentum of the system but changes that occurred. You could consider this sum of the momentum changes of Car A and Car B that occurred in the system.

Energy Bar Graphs
- These graphs display changes in kinetic and potential energy over time. External forces alter these trends, indicating energy transfer.
- If there is a change in Mechanical energy before and after then there must me an external force interacting with the system.

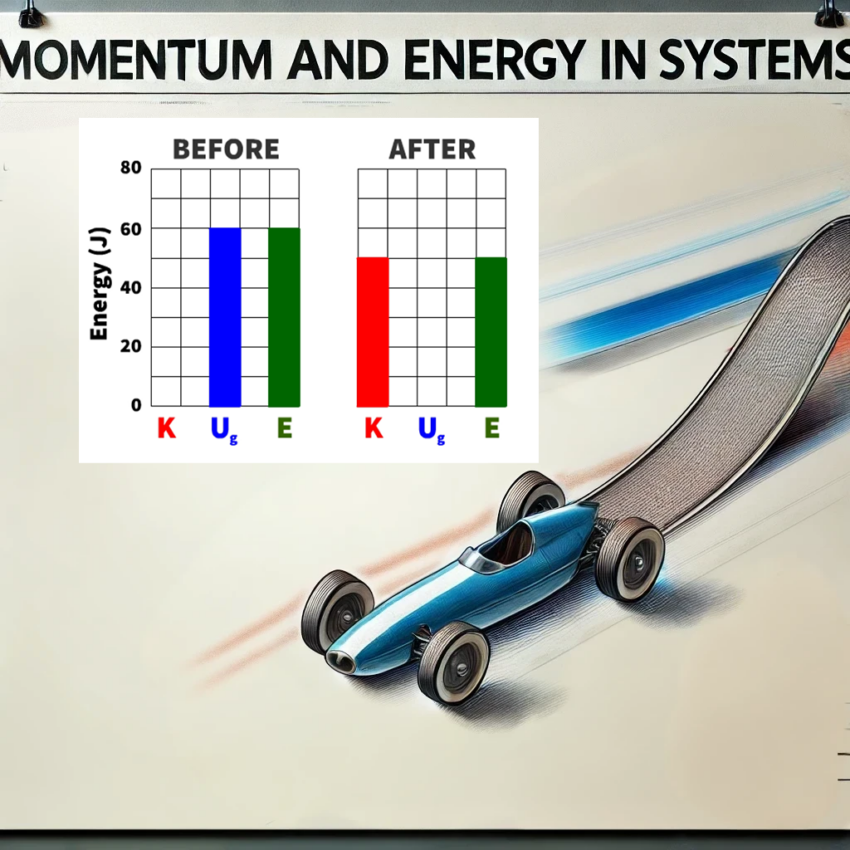
Cart A Rolling Down a Hill
How can you use an energy bar diagram to determine if the track is frictionless?
Cart A is rolling down a hill, with the cart and the Earth defined as the system. This allows us to consider gravitational potential energy (Ug) and kinetic energy (K) as components of the system’s mechanical energy (E). Initially, the cart starts with a certain amount of potential energy at the top of the hill, which is gradually converted into kinetic energy as it rolls downward.

Mechanical Energy Was Lost
The track must have friction because the mechanical energy of the system changed from the top of the hill to the bottom.
As the cart moved downhill, potential energy (Ug) was converted into kinetic energy (K) . However, the total mechanical energy (E) decreased during this process. This indicates that work (W) was done by an external force—friction—which converted some of the mechanical energy into thermal energy, reducing the overall mechanical energy of the system.
Combined Graph Analysis
By combining momentum and energy graphs, you can cross-reference changes to detect external forces.
Historical Example: The Discovery of Neptune
A pivotal moment in physics history involved the discovery of Neptune in 1846. Astronomers observed that Uranus’s orbital momentum and energy deviated from predictions, suggesting an external gravitational influence. Calculations led to the prediction and eventual confirmation of Neptune, demonstrating the power of analyzing momentum and energy to uncover hidden forces.
Practice Questions
Question 1: A ball bounces off the ground, but each bounce is lower than the previous one. Why is mechanical energy not conserved?
Question 2: A satellite’s trajectory shifts as it passes near a planet. What explains this?

Question 3: What is the change of momentum that results from the changing force in the graph for 0.3 seconds?

Question 4: What is the change of momentum that results from the changing force in the graph for 0.6 seconds?
Momentum and Energy in Systems Conclusion
Momentum and energy in systems reveal the effects of external forces on motion and interactions. By defining systems, analyzing internal and external forces, and utilizing graphs, physicists can identify hidden dynamics and uncover deeper truths about the universe. Whether it’s detecting friction in everyday scenarios or discovering a planet through orbital anomalies, understanding these principles is key.
For more on momentum and energy in systems, visit StickmanPhysics.com for interactive lessons and resources.