Interactions with Weight, Normal Force, and Tension (Multiple Blocks)
Follow equilibrium situations that have multiple box Interaction. Create equilibrium equations to solve problems on a surface or hanging.
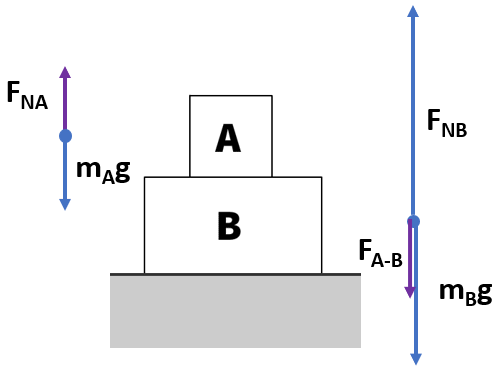
Box A on top of box B on the ground in equilibrium
What are the common force magnitudes in this scenario:
- The weight mAg is a field force on A but equal in magnitude to the contact force (FA-B) which is the push of A down on box B.
All boxes are not moving in equilibrium (ΣF = 0 N in equilibrium)
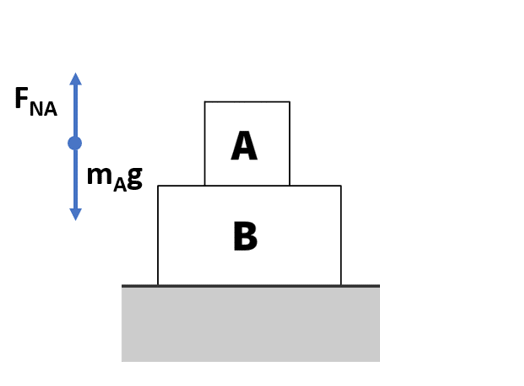
Forces on box A with up being positive:
- Fg: -mAg
- +FNA
ΣF = FNA – mAg
- ΣF = 0 N in equilibrium
0 = FNA – mAg
FNA = mAg
This derivation shows that the normal force which is equal to the force B pushes on A (FB-A) is equal to the weight of Box A.
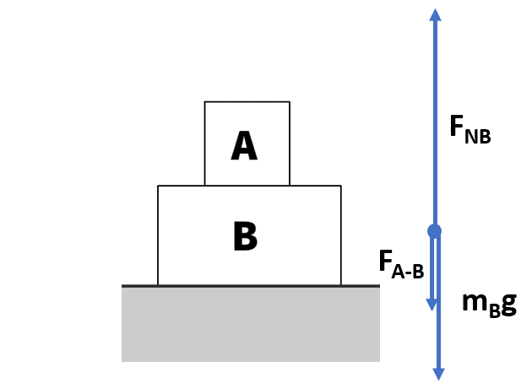
Forces on box B with up being positive:
- Fg: -mBg
- FA-B: -mAg
- +FNB
ΣF = FN – FA-B – mBg
- ΣF = 0 N in equilibrium
0 = FNB – FA-B – mBg
FA-B = FNB – mBg
This derivation shows that the force of A pushing on B is equal to the the normal force pushing up on B minus the weight of box B.
FNB = FA-B + mBg
This derivation shows that the normal force pushing up on B is equal to the force A pushes down on B plus the weight of box B.
Further substitution since magnitude of FA-B = mAg
ΣF = FN – mAg – mBg
- ΣF = 0 N in equilibrium
0 = FNB – mAg – mBg
FNB = mAg + mBg
This derivation shows that the normal force pushing up on B is equal to the weight of both masses combined.
Two Boxes Hanging and Tension
What are the common force magnitudes in this scenario:
- B is hanging with a tension up of (FT B-A) which is equal to box B’s pull down on A.
- Box A is pulling B up by (FT A-B) which is equal and opposite to (FT B-A).
All boxes are in equilibrium (ΣF = 0N in equilibrium)
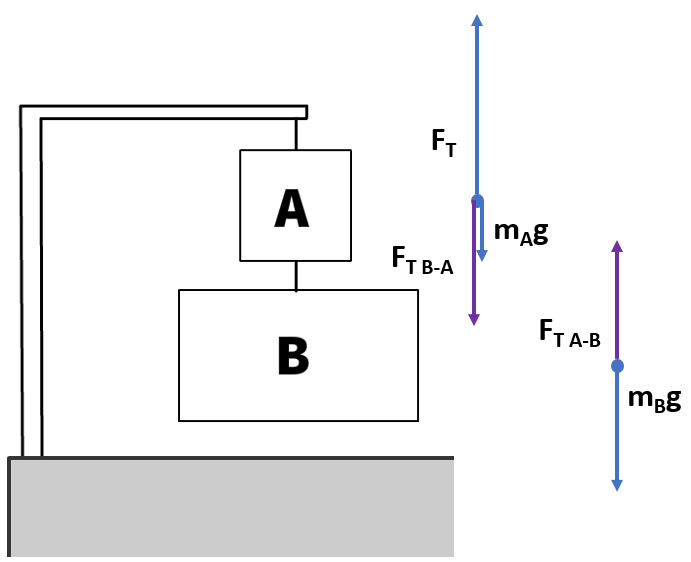
Forces on box A with up being positive:
- Fg: -mAg
- -FT B-A
- +FT
ΣF = FT – mAg – FT B-A
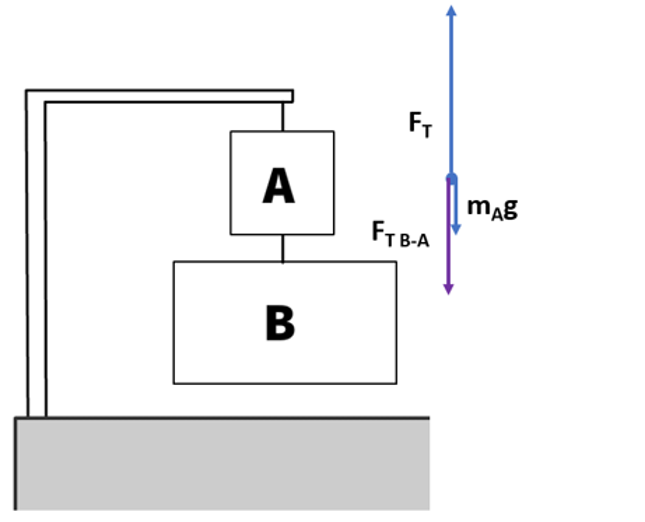
- ΣF = 0N in equilibrium
0 = FT – mAg - FT B-A
FT = mAg + FT B-A
The tension in the rope above box A is equal in magnitude to the weight of box A plus the tension of box B pulling A down
FT B-A = FT – mAg
The tension in the rope below A is equal to the tension in the rope above A minus the weight of box A.
Forces on box B with up being positive:
- Fg: -mBg
- FT A-B
ΣF = FT A-B – mBg
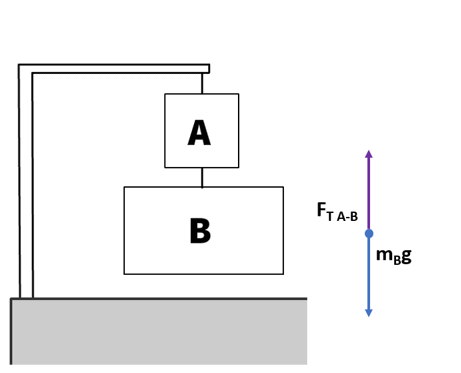
- ΣF = 0N in equilibrium
0 = FT A-B – mBg
FT A-B = mBg
The tension in the rope above box B is equal to the magnitude of box B's weight.
Further substitution
- FT B-A = FT – mAg
- FT A-B = mBg
Since FT B-A = FT A-B = mBg
mBg = FT – mAg
FT = mAg + mBg
The tension in the rope above box A is equal to the weight of box A and box B combined.
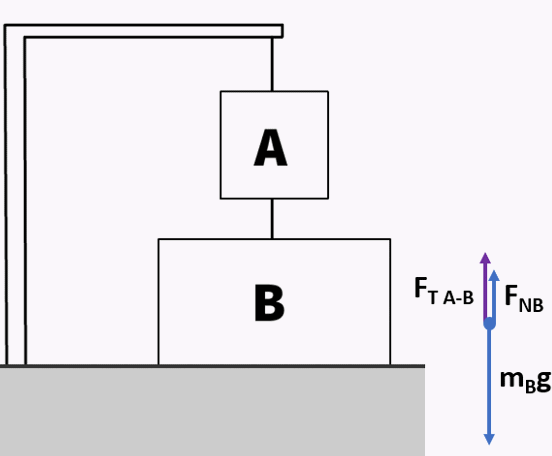
Two Boxes Hanging with Tension and Normal Force
Box A hanging with box B hanging below on the ground in equilibrium
What are the common force magnitudes in this scenario:
- B is hanging with a tension up of (FT B-A) which is equal to box B’s pull down on A.
- Box A is pulling B up by (FT A-B) which is equal and opposite to (FT B-A).
- This is less than the previous scenario because of the ground applying some force up on block B lessening the amount of tension in the rope between block A and B.
***note: my FT A-B subscript represents the force of tension from the block A side of the rope on block B.
Forces on box A with up being positive:
- Fg: -mAg
- -FT B-A
- +FT
ΣF = FT – mAg – FT B-A
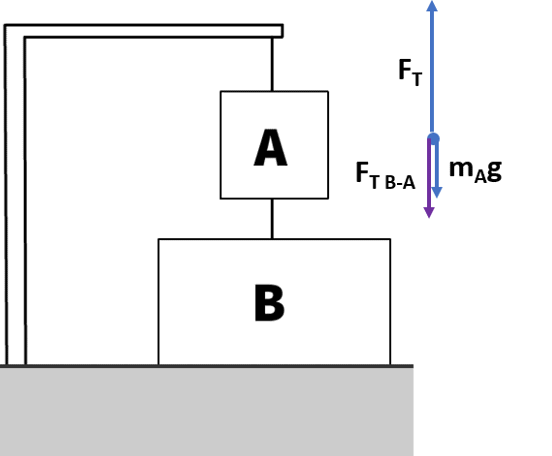
This scenario is the same as the prior but there will be less pull down as a result of box B on the ground with normal force.
- ΣF = 0N in equilibrium
0 = FT – mAg - FT B-A
FT = mAg + FT B-A
The tension in the rope above box A is equal in magnitude to the weight of box A plus the tension of box B pulling A down
FT B-A = FT – mAg
The tension in the rope below A is equal to the tension in the rope above A minus the weight of box A.
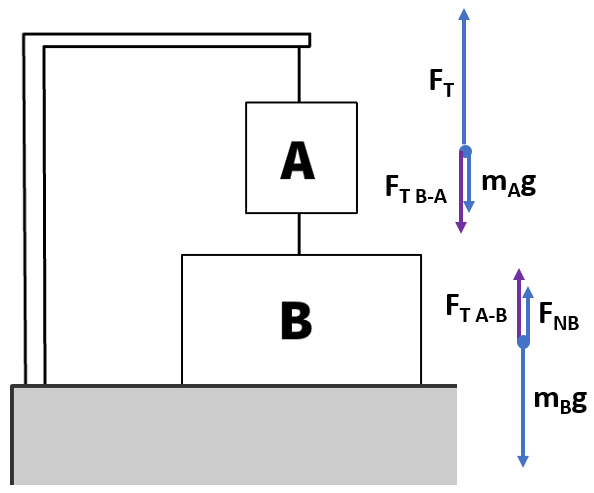
Forces on box B with up being positive:
- Fg: -mBg
- +FT A-B
- +FNB
ΣF = FT A-B + FNB – mBg
- ΣF = 0N in equilibrium
0 = FT A-B + FNB – mBg
FT A-B = mBg - FNB
The tension in the rope above box B is equal to the magnitude of box B's weight minus the normal force of the ground pushing up.
FNB = mBg - FT A-B
The normal force of the ground pushing up is equal to the magnitude of the weight of box B minus the tension in the rope above B.
Further substitution:
- FT B-A = FT – mAg
- FT A-B = mBg - FNB
FT = mAg + FT B-A
The tension above box A is equal to the magnitude of box A's weight plus the tension in the rope below A.
Since FT B-A = FT A-B = mBg - FNB
FT = mAg + mBg - FNB
FT = g(mA + mB) - FNB
After a little more rearranging you see the tension above box A is equal to the combined weight of box A and B minus the normal force below box B.
Links
- Forward: Atwood Machines with Two Hanging Masses
- Back to Weight Normal Force and Tension (Single Block)
- Back to the Main Forces Page
- Back to the Stickman Physics Home Page
