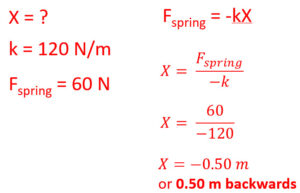Hooke's Law and Spring Force

Home » Unit 3: Newton’s Laws of Motion and Force » Hooke’s Law and Spring Force

Learn how Hooke's Law relates a spring to the force required to stretch it a certain distance using the equation F_spring = -kx.

Hooke's Law Equation

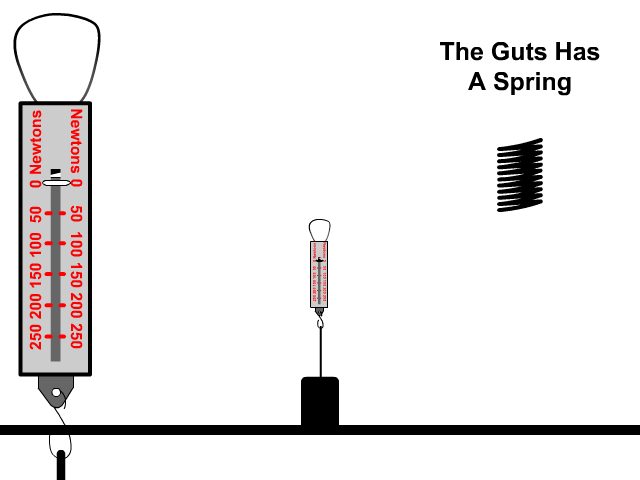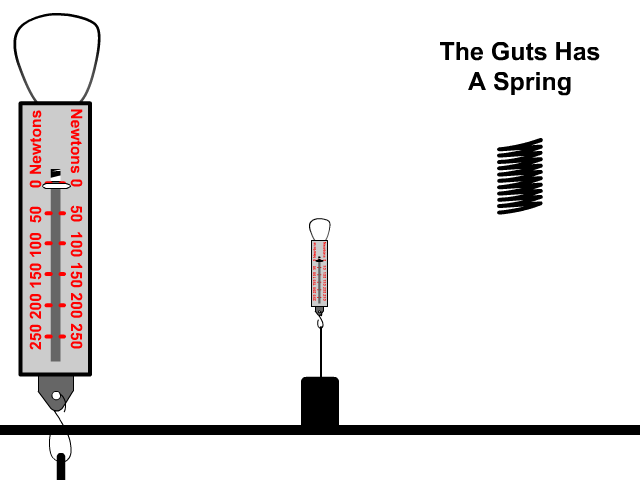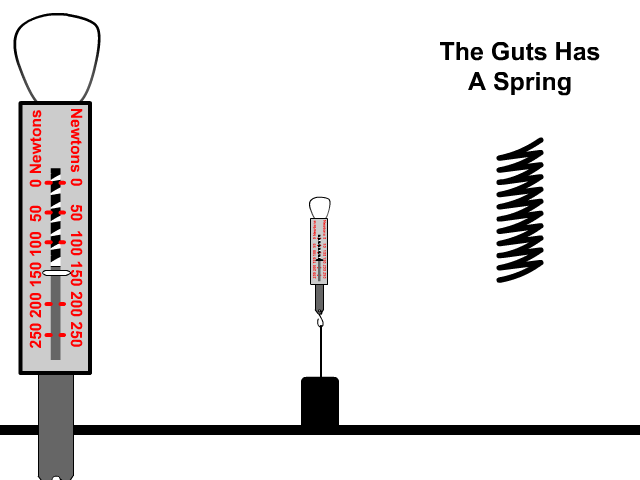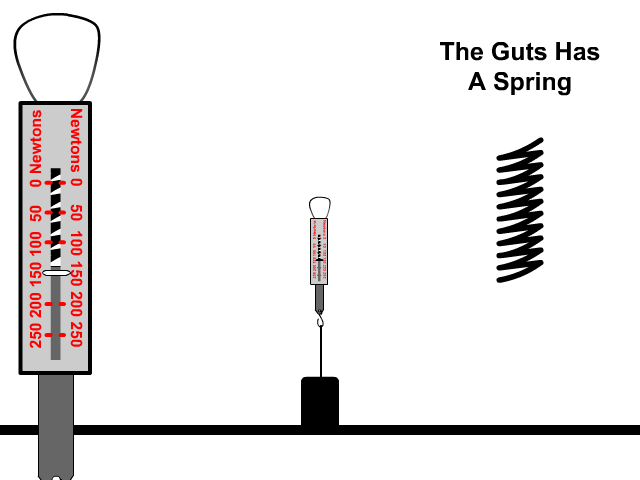
A spring scale works by using a spring that is stretched to measure how much force present that caused the stretch.

Hooke’s Law: F_spring= -kX

F_spring= force in the spring (N)

Also called restoring force which always points in the opposite direction of the displacement.
The spring wants to restore itself to its equilibrium or normal length

k= spring constant: relates the force on the spring to displacement (unit: N/m)

X= displacement of a spring (m) away from the origin

Displacement describes how far the spring was either stretched or compressed

Since the spring will stretch away from an original point we will use negative values for displacement.

The Spring Constant (k)

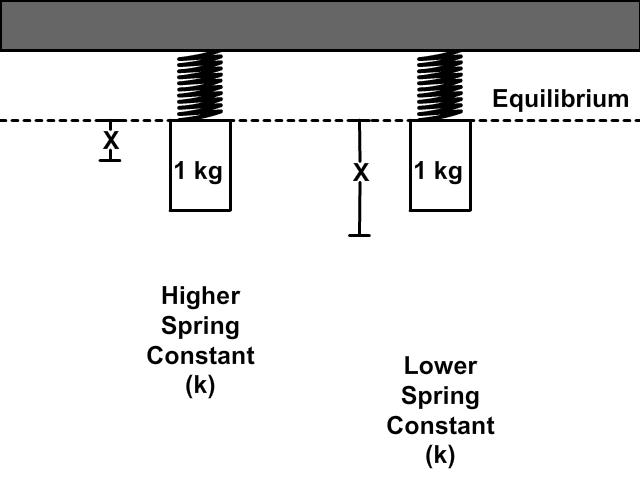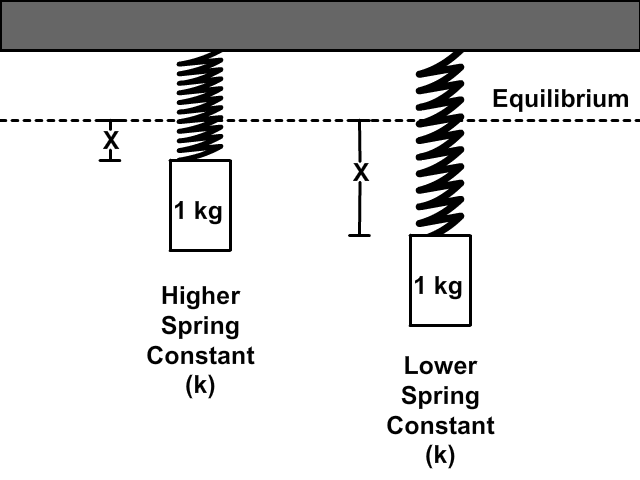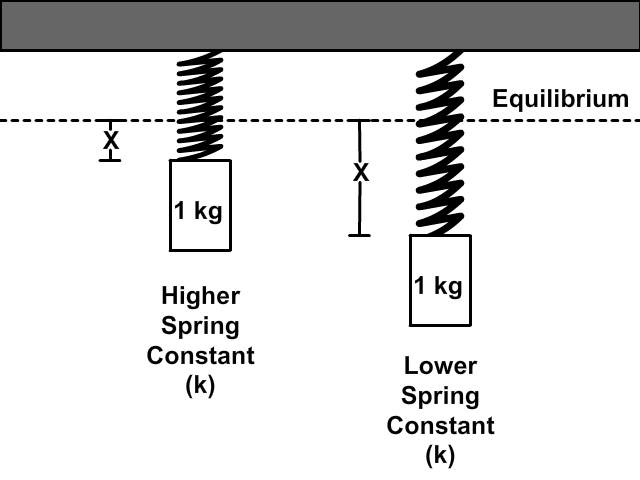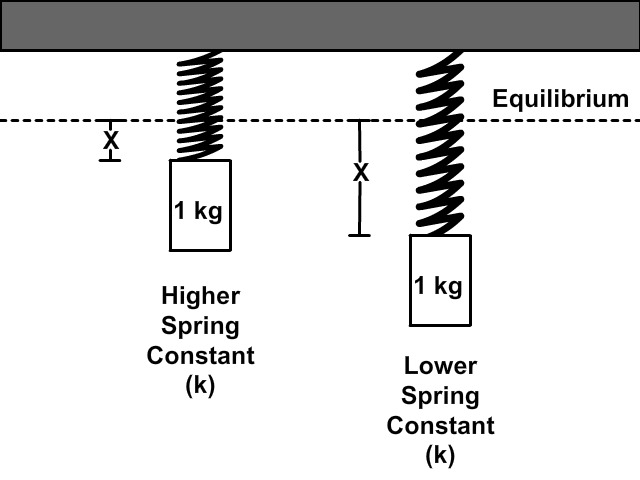
A spring wants to maintain its shape at an equilibrium, non-stretched position. It requires a force to change this equilibrium position. The amount of force required is determined by the spring constant (k).

The spring constant (k) is determined by the material content of the spring, its thickness, and elasticity.

Elasticity of a material is the resistance to a change in shape.

The higher the spring constant, the more elasticity, and the less a spring will stretch when the same force is present.

Springs that resist change, and therefore have a higher elasticity are more stiff than those with less elasticity.

Questions

Q1: Which would take more force to displace? A spring with a spring constant of 30 N/m or one with a spring constant of 60 N/m

60 N/m , the higher the value the more elastic or resistant to change

Q2: How much force is required to stretch a string by 0.5 meters that has a spring constant of 50 N/m?

F_spring = ?

X = -0.5 m

k = 50 N/m

F_spring = -kX

F_spring = -(50)(-0.5)

F_spring = 25 N

Q3: How much would a spring stretch that has a spring constant of 120 N/m when pulled with 60 N of force?

Graphical Representation of Spring Constant

F_spring = -kx

rearranged becomes

k = (-F_spring)/(x)

Slope = (rise)/run)

In the graph the rise is Newton's (N) of force and run is meters (m) of displacement. The slope becomes N/m the unit for spring constant.

The slope of a spring force vs. displacement graph is equal to the spring constant

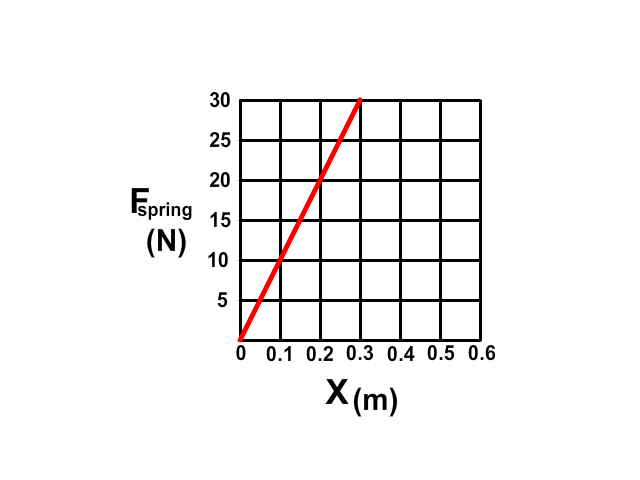
Q4: What is the spring constant represented by the graph?

Q5: How much mass would be required to stretch this spring 0.9 m?

k = 100 N/m

F_spring = ?

X = -0.9 m

F_spring = -kx

F_spring = -(100)(-0.9) = 90 N

F_spring = F_w

F_w = mg

F_spring = mg

m = F_spring / g

90/10 = 9 kg

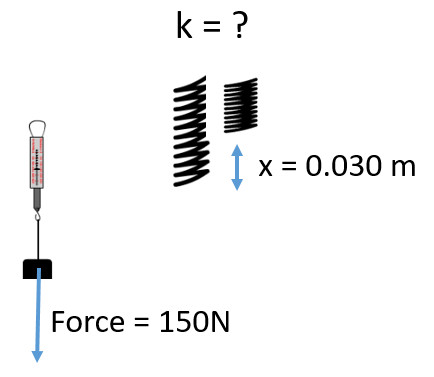
Q6: How much is the spring constant in a spring that requires 150 N of force to displace it 0.030 m from the origin?

341

Hooke's Law and Springs Quiz

1 / 4

What happens to the magnitude of force required to stretch a spring 0.1 m when the spring constant increases?

force must increase

force must decrease

force stays the same

2 / 4

How much force is in a spring that has a spring constant of 4400 N/m that is displaced 0.03 m?

102 N

65 N

321 N

132 N

3 / 4

What is the spring constant of a spring displaced 0.1 meters when 400 N of force is applied?

40 N/m

4000 N/m

384 N/m

10 N/m

4 / 4

What is the displacement of a spring that has a spring constant of 2000 N/m when a force of 500N is applied?

0.25 m

1000000 m

2.5 m

4 m

Your score is